Marching Cubes is an algorithm for rendering isosurfaces in volumetric data. The basic notion is that we can define a voxel(cube) by the pixel values at the eight corners of the cube. If one or more pixels of a cube have values less than the user-specified isovalue, and one or more have values greater than this value, we know the voxel must contribute some component of the isosurface. By determining which edges of the cube are intersected by the isosurface, we can create triangular patches which divide the cube between regions within the isosurface and regions outside. By connecting the patches from all cubes on the isosurface boundary, we get a surface representation.
This algorithm is often used to extract the surface of medical organs. It provides a fast and easy way to get from serial sections to a complete 3D object.

	Because three dimensional surfaces of the anatomy offer a useful medical tool, marching cubes algorithm is mainly used to process medical data. Typically, these data are acquired by computed tomography (CT), magnetic resonance (MR) or single photon emission computed tomography (SPECT), and marching cube algorithm allows visualization of complex models (see : Improvement of shoulder replacement surgery by image processing).
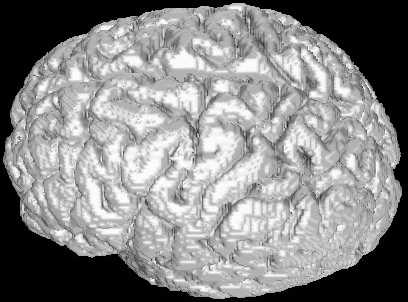
^- On the top picture you can see a human brain surface reconstructed by using marching cubes (128984 vertices and 258004 triangles) The picture above show a magnified display of brain surface constructed by using marching cubes. ~>
Nevertheless, it can be used in many other fields, like metaballs modelling, which is very useful to organic behaviour simulations. Marching cubes has also the valuable advantage that it's a high-resolution 3D surface construction algorithm that can be displayed using conventional graphics rendering methods, as we'll see in the practical approach section. Metaballs exemple. ~>