Synthèse d'images, Java3D

• Introduction
• Un univers simple de Java3D
• TD1: un univers simple
• TD2: un univers pas si simple
• TD3: que la lumière soit
• TD4: interaction
• Mini projet
• Sujets d'examen

Qu'est-ce que Java3D? Qu'est-ce que n'est pas java3D

Java3D est une bibliothèque logicielle de haut niveau facilitant la création, la visualisation et la manipulation de scènes 3D. Java3D fournit une API en java et bénéficie donc de la portabilité de ce langage. Java3D est porté sur différentes plateformes. Il utilise (de manière transparente pour l'utilisateur) des bibliothèques graphiques de plus bas niveau telles qu'OpenGL ou DirectX pour réaliser le rendu 3D.

Java3D n'est pas un modeleur (tel que 3D studio): il n'offre aucun support pour l'édition d'objet et de scènes 3D. Il permet en revanche de programmer son propre modeleur à moindre coût. Java3D n'est pas non plus un format de données 3D (tel que VRML): certaines fonctions d'importation/exportation vers différents formats standards existent mais Java3D ne défini pas en soi de format particulier.

Le principales fonctionnalités de Java3D sont:

• Le calcul vectoriel et matriciel (matrices 3x3 et 4x4).
• La représentation d'objets 3D (géométrie et apparence).
• L'assemblages d'objets dans un graphe de scène.
• La visualisation du graphe de scène à travers un moteur de rendu.
• L'interface avec différents périphériques d'entrée (souris classique, souris 3D, ...) et de sortie (écran, casque vidéo...)
• Les sons 3D
• L'animation
• La détection de collisions
• ...

Références

• Page principale de Java3D (incluant les implémentation windows et solaris)
• Implémentation de Java3D sous linux
• Un tutorial
• Le guide de la version 1.3
• Le guide en ligne de la version 1.2
• Le quide de référence de l'API Java3D (packages javax.media.j3d et javax.vecmath).
• Le guide de référe,ce de l'API complémentaire de SUN (package com.sun.j3d.utils)

Compilation et exécution de programmes en Java3D

L'utilisation de Java3D nécessite que les packages javax.media.j3d, javax.vecmath, et com.sun.j3d.utils soient installés sur votre système. Ces classes sont disponibles sous formes d'archives: j3dcore.jar, j3daudio.jar, j3dutils.jar et vecmath.jar. Nous utiliseront une implémentation spéciale de java installée dans /net/opt/blackdown-jdk-1.4.2.0 qui supporte une version 1.3.1 de l'API java3D. L'API elle même est installée dans /net/opt/blackdown-java3d-bin. Pour le bon fonctionnement de java 3D vous devrez:

1. Assurer l'accès aux jar de java3D:
   export CLASSPATH=/net/opt/blackdown-java3d-bin/lib/j3dcore.jar:/net/opt/blackdown-java3d-bin/lib/j3daudio.jar:/net/opt/blackdown-java3d-bin/lib/j3dutils.jar:/net/opt/blackdown-java3d-bin/lib/vecmath.jar:.:${CLASSPATH}
2. Ajouter le chemin des librairies dynamiques de java3D lors de l'exécution des programmes:
   alias java='java -Djava.library.path=/net/opt/blackdown-java3d-bin/lib'

Dans vos fichiers java, vous devrez importer les packages:

import javax.media.j3d.*;
import javax.vecmath.*;
import com.sun.j3d.utils.universe.*;

javac *.java
java MaClassePrincipale

Tout un univers

Un programme Java3D décrit un univers virtuel qu'il est possible de visualiser et dans lequel on peut naviguer. La structure fondamentale de java3D est la classe VirtualUniverse contenant à la fois la description du contenu de la scène 3D à visualiser et les informations de visualisation. Dans un premier temps nous utiliserons une classe dérivée simplifiée nommée SimpleUniverse.

L'univers virtuel de Java3D est construit de telle sorte qu'il permette la représentation de l'univers physique connu: il utilise un système de coordonnées de haute précision vous permettant de représenter 2 noyaux atomiques situés aux confins de l'univers si vous le désirez. Afin d'obtenir une telle précision, les nombres flotants à double précision classiques (encodés sur 64 bits) ne sont pas suffisants. Java3D définit des flotants à haute précision (classe HiResCoord) encodés sur 256 bits. Un objet de localisation (classe Locale) définit une origine locale dans l'univers virtuel à partir d'une translation haute précision. Localement, autour de l'origine définie par un Locale, les coordonnées en double précision classiques sont suffisante pour représenter tous types d'objet. La figure 1 représente un univers virtuel dans lequel ont été ajouté 4 Locales différentes. Dans l'exemple ci-dessus, les deux atomes appartiendraient à deux Locales différents dont les origines sont positionnées aux confins de l'univers virtuel mais leur position et leur géométrie pourrait être représentée localement avec des nombres en double précision. La grande majorité des programmes Java3D n'utilise qu'un objet de type Locale dans lequel sont représentés tous les objets de l'univers virtuel mais dans certains cas il peut devenir nécessaire de faire appel à plusieurs Locales.

Figure 1. Exemple d'univers virtuel contenant 4 Locales. Chaque Locale représente un système de coordonnées locales décalée d'une translation par rapport au système de coordonnées global.

Le graphe de scène

Dans chaque Locale, les objets 3D composant la scène manipulée sont représentés dans un graphe de scène. Un graphe de scène est un graphe direct acyclique dont la racine est l'univers virtuel et composé de noeuds représentant des transformations 3D ou des groupes d'objets graphiques. Aux feuilles de ce graphes sont décrit les objets graphiques. Un graphe de scène étant acyclique et direct (orienté dans un seul sens), il existe un seul chemin de la racine vers chaque feuille. Le parcours de ce chemin déterminera comment l'objet graphique de chaque feuille sera représenté (après possibles transformations géométriques ou étapes de contrôle du rendu). La figure 2 représente un graphe de scène minimal. Dans l'univers virtuel, un seul système de coordonnées locales a été défini. A cette origine est attachée une branche (classe BranchGroup). Il pourrait y avoir différentes branches décrivant différentes sous-parties du graphe de scène. La branche contient une noeud de transformation géométrique (classe TransformationGroup). Sous le noeud de transformation se trouve une feuille du graphe: un objet graphique. Lors de la visualisation de cette scène, la géométrie de l'objet graphique sera conditionnée par les noeuds rencontrées lors du parcours de la branche menant à cette feuille: ses coordonnées seront translatées selon le systèmes de coordonnées locales puis transformées par la transformation 3D de l'avant dernier noeud.

Figure 2. Un exemple minimal de graphe de scène: un univers virtuel définissant une système de coordonnées locales dans lequel une branche contient un noeud de transformation et une feuille.

La chaîne de visualisation

Le graphe de scène permet de décrire une scène 3D, de la plus simple (telle que celle représentée dans la figure 2) à la plus complexe (en garnissant le graphe de scène de branches multiples). Il manque encore un élément essentiel à la réalisation de tout programme Java3D: la visualisation. La visualisation est composée de deux éléments:

• un point de vue (classe ViewPlatform) qui définit l'angle sous lequel est vue la scène 3D;
• une interface avec la fenêtre de visualisation (définition des paramètres de l'oeil virtuel: classes Viewer et Canvas3D).

Le point de vue est considéré comme une feuille du graphe de scène: il se trouve au bout d'une branche classique du graphe. L'interface de visualisation est composée d'objets n'appartenant pas vraiment au graphe de scène mais faisant la liason entre la feuille "point de vue" et la fenêtre de visualisation. La figure 3 illustre un graphe de scène complet incluant une branche de visualisation.

Figure 3. Un exemple de graphe de scène complet incluant une branche de visualisation et son interface avec le sytème graphique.

Le point de vue (ViewPlatform) est en bout d'une branche du graphe de scène. Le noeud juste au dessus est une transformation 3D définissant sa position. L'objet ViewPlatform dispose d'une référence sur un objet de type View. View est la classe centrale de la chaîne de visualisation. Elle établit un lien entre le graphe de scène (en référençant l'objet ViewPlatform), la fenêtre de visualisation (de type Canvas3D, héritant de java.awt.Canvas) et la représentation virtuelle de l'oeil regardant la scène et de son environnement (classes PhysicalBody et PhysicalEnvironement).

La création d'un graphe de scène et d'une chaîne de visualisation complète offrent une grande liberté mais sont aussi assez fastidieuses en raison du nombre d'objets manipulés. La majorité des applications simples ne nécessitent pas toute la souplesse que peut offrir Java3D et peuvent se contenter d'une version simplifiée de l'univers virtuel et des classes qui lui sont rattachées. A cet effet, la classe SimpleUniverse, dérivée de VirtualUniverse, a été écrite dans le package com.sun.j3d.utils. Un univers simple englobe toute la branche de visualisation du graphe de scène et la chaîne de visualisation associée comme illustré dans la figure 3.

TD1: un univers simple

Dans les étapes suivantes, vous allez écrire votre premier programme Java3D: vous ferez afficher un cube tournant aux facettes colorées tel que représenté dans la figure 4 ci-dessous:

Figure 4. Un univers simple de Java3D: un cube coloré visualisé à travers une fenêtre graphique.

1. Ecrivez une application java dans laquelle vous créerez un objet de type SimpleUniverse. Créez une branche du graphe de scène dans lequel vous pourrez attacher le cube. La méthode void SimpleUniverse.addBranchGraph(BranchGroup) vous permettra de connecter la branche à votre univers. L'objet cube coloré est disponible dans la classe com.sun.j3d.utils.geometry.ColorCube. Chaque groupe (i.e. chaque noeud qui n'est pas une feuille) du graphe de scène dispose d'une méthode addChild permettant d'ajouter un fils au groupe concerné. Une fois le graphe de scène complet, vous devrez définir la position du point de vue de façon à se que l'oeil virtuel regarde la scène depuis un point extérieur. Vous ferez appel pour cela à la commande: mySimpleUniverse.getViewingPlatform().setNominalViewingTransform(). Vous pourrez enfin créer une Frame de l'AWT java dans laquelle vous ajouterez une fenêtre de type Canvas3D. Le constructeur de Canvas3D nécessite un objet de configuration de type java.awt.GraphicsConfiguration. Vous pouvez créer un objet de configuration standard par appel à la commande: SimpleUniverse.getPreferredConfiguration(). Votre premier programme est complet: vous devez être à même de visualiser le cube. Comme celui-ci est vu de face, un seul carré (rouge) apparaît à l'écran.
2. Afin de visualiser le cube sous un autre angle, vous allez modifier votre graphe de scène. Ajoutez un noeud de type TransformGroup entre la racine de la branche et le cube. Le constructeur de TransformGroup prend en paramètre une transformation 3D (composition d'une translation, d'une rotation et d'un facteur d'échelle) de type Transform3D. Faîtes appel aux méthodes rotX, rotY, rotZ et mul de Transform3D pour composer des rotations selon les axes X, Y, et Z. Modifiez votre programme pour prendre 3 angles sur la ligne de commande et utiliser ces angles dans la composition de la transformation. Vérifiez que la visualisation du cube est bien celle que vous attendez sous différents angles. Déterminez la direction des axes dans le repère par défaut de Java3D. Identifiez quelle face (couleur) correspond à quelle direction.
3. Afin d'optimiser la visualisation du graphe de scène, Java3D fait certaines hypothèses et impose certaines contraintes sur la création et le manipulation de ce graphe. Chaque branche du graphe peut être active ou inactive (alive). Chaque branche peut également être compilée (compiled) c'est-à-dire transformée dans une représentation interne qui facilite sa manipulation. Un branche devient active dès qu'elle est ajoutée dans le graphe de scène. Il est impossible de modifier une branche une fois qu'elle est devenue active: vous devez d'abord construire toute la branche puis l'ajouter au graphe. Une exception sera jetée si vous tentez de modifier une branche déjà intégrée au graphe de scène. La compilation est un acte explicite: appelez la méthode GraphBranch.compile pour compiler une branche. Les propriétés d'une branche compilée ne peuvent plus être modifiée à l'exception des propriétés qui ont explicitement été déclarées modifiables AVANT la compilation. Tenter de modifier une propriété non modifiable ou de déclarer une nouvelle propriété modifiable après compilation provoque une exception. Compilez votre graphe de scène. Tentez de lire la matrice de transformation 3D qui positionne le cube coloré. Ajoutez maintenant la capacité "lecture de transformation" au groupe de transformation par l'intermédiaire de la méthode TransformGroup.setCapability avant compilation. Vérifiez que cela ce passe mieux.
4. Remplacez le cube prédéfini com.sun.j3d.utils.geometry.ColorCube par votre propre forme 3D. Une forme 3D hérite de la classe Shape3D. Une forme 3D est définie par sa géométrie et son apparence. Nous ne nous intéresserons qu'à la géométrie pour l'instant: créez un objet de type QuadArray représentant la géométrie d'un cube et ajoutez le dans votre forme 3D par l'intermédiaire de la méthode Shape3D.setGeometry.
5. Vous allez maintenant animer le cube d'un mouvement de rotation autour de l'axe Y. Ajoutez comme fils du groupe de transformation un interpolateur de type RotationInterpolator. Un interpolateur transforme le temps en une grandeur physique changeante telle qu'une matrice de rotation dans ce cas. Un interpolateur fait appel à une représentation intermédiaire (un objet de type Alpha) et, pour des raisons d'optimisation, à une boite englobante: un interpolateur n'est activé que si sa boite englobante est visible. Vous pouvez créer plusieurs objets englobants. Dans cet exemple, un objet de type BoudingSphere conviendra. Une objet de type Alpha définit la fonction de transformation du temps en valeur entre 0 et 1: vitesse, répétitivité, et éventuellement définition d'une fonction complexe de transformation.
6. Votre cube s'est mis à tourner autour de l'axe Y mais vous avez probablement perdu la rotation initiale du cube et vous visualisez donc toujours le cube en rotation de face. Pourquoi? Modifiez votre code pour permettre la visualisation sous un angle initial déterminé par la ligne de commande.

Ce second TD consiste à créer un univers virtuel complet sans faire appel à la classe SimpleUniverse.

1. Reprenez le code du TD1 et supprimez l'importation du package com.sun.j3d.utils. Remplacez la création du SimpleUniverse par un VirtualUniverse. Créez un Locale et une branche de visualisation complète. Vous devrez en particulier veiller au positionnement de l'oeil virtuel, en vous appuyant sur votre connaissance du repère par défaut. Créez la chaîne de visualisation complète et assurez que votre univers pas si simple remplit la même fonction que l'univers simple du TD1.
2. Ecrivez une nouvelle classe Viewer3D intégrant une fenêtre graphique et toute la chaîne de visualisation. Vérifiez que vous savez afficher plusieurs vues de la même scène 3D sous différents points de vue.
3. Jouez sur les paramètres de point de vue et de taille respective du cube. Vérifiez qu'il n'y a pas de différence entre un gros cube vu de loin et un petit cube vu de près.
4. Ajoutez un second cube dans votre scène.

Le cube que nous avons visualisé dans les TDs précédents n'est pas réaliste: chacune de ses faces est peinte d'une couleur unique et invariante, quel que soit le point de vue de l'utilisateur et l'éclairage. Nous allons améliorer le rendu d'une scène par l'ajout de lumières, le contrôle des matériaux dont sont composés les objets et le plaquage de textures. Le but de ce TD est de réalisé le rendu d'une scène telle que:

Lumières et matériaux

1. En repartant du TD précédent, affichez un cube et une sphère. Une sphère est approximée par un maillage triangulé de forme sphérique. La classe com.sun.j3d.utils.geometry.Sphere vous simplifie la tâche en définissant un objet héritant de Group et générant la géométrie voulue. Vous devrez transmettre au constructeur de Sphere un objet de type Appearance que vous aurez créé au préalable. La sphère s'affiche en blanc: il s'agit de la couleur par défaut et en l'absence d'éclairage le facettes ne sont pas colorées.
2. L'objet Appearance est complémentaire de l'objet Geometry pour les formes 3D: il contrôle la manière dont doit s'afficher la géométrie spécifiée (matériaux des faces, transparence, etc). Créez un objet de type Material que vous associerez à l'objet d'apparence par la méthode Appearance.setMaterial. Le matériau d'un objet est défini comme en OpenGL par ses caractéristiques "ambiante", "émissive", "diffuse", "spéculaire" et de brillance. Après définition du matériau de votre sphère, elle est affichée en noir: un matériau lui est attribuée mais elle n'est pas éclairée.
3. Ajoutez dans la scène une lumière ambiante (fond lumineux de la scène) en créant un objet de type AmbientLight et en l'ajoutant au graphe de scène en tant que fils du même noeud que votre sphère. Une lumière ajoutée dans une branche du graphe de scène illumine tous les objets de cette branche indépendament du noeud auquel elle appartient. La portée d'une lumière est cependant bornée par un objet englobant (héritant de la classe Bounds). Ceci permet, par exemple, d'empêcher un lumière définie à l'intérieur d'une pièce d'illuminer les objets se trouvant à l'extérieur. Dans cet exercice, vous pouvez créer une sphère englobante (classe BoundingSphere) et l'associer à la lumière ambiante par la méthode AmbientLight.setInfluencingBounds. Le rendu s'améliore: la sphère apparaît désormait dans une couleur uniforme correspondant à la composition de la composante ambiante du matériaux et à la couleur de la lumière ambiente (blanche par défaut).
4. Afin de prendre en compte les composantes diffuses et spéculaires du matériau, ajoutez une lampe de type DirectionalLight à votre scène. Le rendu devient réaliste.
5. Vérifiez que vous pouvez réaliser un rendu plat, par opposition au rendu de type Gouraud réalisé par défaut, en créant un objet de type ColoringAttributes que vous ajouterez à votre objet de type Appearance.
6. Créez un objet de type TransparencyAttributes et réalisez le rendu de la sphère en transparence.

Texture

1. Remplacez le cube coloré par un simple quadrilatère correspondant à l'une de ses faces. Vous allez plaquer une texture sur cette surface.
2. Pour plaquer une texture, il est nécessaire de préciser des coordonnées de texture pour chaque coordonnée 3D fournie. Une coordonnées de texture est une coordonnées 2D indiquant quel pixel de l'image de texture doit se plaquer sur un point 3D de la scène. La génération des coordonnées de texture est activée, pour les primitives géométrique de type QuadArray si vous précisez le format TEXTURE_COORDINATE_2 à la création de l'objet.
3. Chargez l'image de texture. Une image de texture doit nécessairement avoir pour taille n*n où n est une puissance de 2. Redimensionnez votre image en conséquence. Depuis la JDK 1.4, la classe javax.imageio.ImageIO permet de créer un objet de type BufferedImage à partir d'un nom de fichier image. Avec une JDK antérieure, vous pouvez utiliser le code de la classe ImageIO ci-dessous.
4. Créez un objet de type ImageComponent2D (du package javax.media.j3d) à partir de l'image chargée.
5. Créez un objet de type Texture2D et associez lui la composante d'image par la méthode Texture2D.setImage.
6. Enfin, créez un objet de type Appearance auquel vous assignerez votre texture par la méthode setTexture et que vous affecterez à votre face. La face texturée doit s'afficher dans votre scène.
7. Recréez un cube dont toutes les faces sont texturées.

class ImageIO {

  public static BufferedImage read(String filename) {
    java.awt.Container observer = new java.awt.Container();
    Image image = Toolkit.getDefaultToolkit().createImage(filename);

    observer.prepareImage(image, null);
    while(true) {
      int status = observer.checkImage(image, null);
      if ((status & java.awt.image.ImageObserver.ERROR) != 0) {
	return null;
      } else if ((status & java.awt.image.ImageObserver.ALLBITS) != 0) {
	break;
      }
      try {
	Thread.sleep(100);
      }
      catch (InterruptedException e) {
      }
    }
 
    int width = image.getWidth(observer);
    int height = image.getHeight(observer);
 
    int[] bandOffset = { 0, 1, 2, 3};
    java.awt.image.WritableRaster wr =
      java.awt.image.Raster.createInterleavedRaster(
	java.awt.image.DataBuffer.TYPE_BYTE,
	width, height, width * 4,
	4, bandOffset, null);
    int[] nBits = {8, 8, 8, 8};
    java.awt.image.ComponentColorModel colorModel =
      new java.awt.image.ComponentColorModel(
	java.awt.color.ColorSpace.getInstance(
	  java.awt.color.ColorSpace.CS_sRGB),
	nBits, true, false, Transparency.TRANSLUCENT, 0);
    BufferedImage bImage = new BufferedImage(colorModel, wr, false, null);
    java.awt.Graphics g = bImage.getGraphics();
    g.drawImage(image, 0, 0, observer);

    return bImage;
  }

}

Texte

1. Créez un objet de type com.sun.j3d.utils.geometry.Text2D et insérez le dans votre scène pour ajouter du texte.
2. Créez une fonte 3D (classe javax.media.j3d.Font3D) par un appel du type: new Font3D(new Font("Helvetica", Font.PLAIN, 12), new FontExtrusion()) . Utilisez cette fonte pour créer un objet de type Shape3D que vous insérerez dans votre scène pour ajouter du texte en charctères "épais".

Il est temps d'autoriser l'utilisateur à naviguer à travers l'univers virtuel. L'interpolateur utilisé depuis le TD1 permet de faire tourner la scène sous les yeux de l'utilisateur mais celui ci n'a pas de contrôle interactif sur le point de vue qu'il désire prendre. Les objets d'interaction utilisent un mécanisme général de Java3D dénomé comportement (Behavior). Un comportement décrit la modification du graphe de scène en fonction d'un stimulis. Un stimulis peut être de différent type (événement de l'AWT, écoulement du temps, action de m'utilisateur, etc). Un comportement le transforme en différentes modifications du graphe de scène (changement d'une matrice de transformation, de la structure du graphe, etc). Un interpolateur est ainsi un cas particulier de comportement. D'autres comportements permettent de gérer les interactions avec l'utilisateur: navigation et sélection.

Vous allez dans un premier temps utiliser les classes de comportement prédéfinies pour la navigation au clavier et à la souris. Elles sont disponibles dans les packages com.sun.j3d.utils.behaviors.keyboard et com.sun.j3d.utils.behaviors.mouse respectivement.

Navigation

1. Créez un objet de type KeyNavigatorBehavior qui contrôle le noeud de transformation de votre classe Viewer3D. Naviguez dans la scène en 3D en utilisant les flêches, PgUp et PgDn.
2. Créez 3 objets de type MouseRotate, MouseTranslate et MouseZoom. Naviguez dans la scène en 3D en utilisant les combinaisons bouton + déplacement souris.
3. Si vous ouvrez une deuxième fenêtre de visualisation, vous vous appercevrez que les déplacements réalisés dans une fenêtre au clavier ou à la souris se répercutent sur l'autre. Expliquez pourquoi et proposez une solution pour controler indépendament le déplacement de différents yeux virtuels.

Sélection

Après la navigation, la sélection d'objets est la seconde nécessité pour une application interactive 3D. Des classes de haut niveau permettant la sélection et le déplacement (translation, rotation, ou changement d'échelle) d'objets sont disponibles dans le package com.sun.j3d.utils.picking.behaviors.

1. Dans votre application, commentez la navigation à partir de la souris et créez un objet de type PickRotateBehavior que vous ajouterez à la racine de votre graphe de scène. Introduisez 2 objets graphique dans la scène et vérifiez que vous pouvez sélectionner et faire tourner l'un ou l'autre indépendament.
2. Assurez vous que le mécanisme de sélection est fonctionnel lorsque vous utilisez plusieurs vues. Ajoutez un sélecteur en translation et en facteur d'échelle.
3. Ajoutez un menu pour permettre, dans chaque vue, de préciser si les événements souris sont utilisés pour la navigation ou bien pour la sélection.

Trackball

La navigation à la souris telle que réalisée dans la classe MouseRotate ne permet la rotation qu'autour de deux axes. Il est possible de permettre à l'utilisateur des rotations autour de trois axes de manière intuitive en simulant une trackball. Une trackball est une boule virtuelle centrée sur la fenêtre de visualisation et que l'utilisateur ferait tourner selon les trois axes selon le shéma ci-dessous:

A l'intérieur de la boule virtuelle, un déplacement de la souris provoque un rotation autour de l'axe horizontal (déplacement vertical) ou de l'axe vertical (déplacement horizontal). Un déplacement de la souris à l'extérieur de la boule virtuelle provoque une rotation autour de l'axe normal au plan de visualisation.

Afin de simuler le comportement d'une trackball il faut capturer les événements souris, déterminer s'ils correspondent à des rotations en X, Y, ou Z, et appliquer les rotation correspondantes au noeud de transformation de l'oeil virtuel concerné. Java3D permet de définir des comportements dans ce but. Un nouveau comportement hérite de la classe virtuelle javax.media.j3d.Behavior et définit les méthodes initialization et processStimulus. Dans ces méthodes, le comportement doit avant tout indiquer au moteur Java3D les conditions dans lesquels il est activé (sa méthode processStimulus est appelée) par appel à wakeupOn. La condition d'activation est dévalidée à chaque appel à processStimulus et doit donc être explicitement réaffirmée avant la sortie de cette méthode.

1. Créez votre propre classe de comportement Trackball et insérez la dans le graphe de scène en remplacement de la classe MouseRotate.
2. Implémentez la fonctionnalité de trackball dans cette classe.

Au cours des séances suivantes, vous développerez un visualisateur d'images médicales 3D. Vous devrez permettre plusieurs modes de visualisation d'une image 3D et la superposition de structures anatomiques représentées par des surfaces.

Une image 3D est un tableau tridimensionnel de valeurs discrètes d'intensité appelées voxels (par extension des pixels composants les images 2D). Il n'est pas possible de visualiser la totalité du contenu d'une image 3D en une fois mais il existe différentes métodes pour apréhender ce type de données. La plus simple est d'extraire un ensemble de plans à l'intérieur du volume et d'autoriser l'utilisateur à naviguer en les changeant interactivement.

Vous utiliserez comme point de départ les classes de visualisation suivantes qui permettent de charger une image 3D au format INR et d'en extraire un plan orthogonal à l'axe X, Y ou Z de l'image. Des données d'exemple sont disponibles ici. Le format INR est un format simple constitué d'un en-tête de 256 caractères lisible suivit des données images sans compression. Nous travaillerons avec des images encodées sur 8 bits (chaque voxel est représenté par un entier entre 0 et 255 définissant l'intensité de ce voxel). Après décompression de l'archive, vous pouvez compiler (javac *.java) puis exécuter le programme de visualisation sur l'image fournie en exemple:
java Main brain.inr Z 60
coupe le volume par le plan de coordonnées z=60 et affiche l'image:

Dans le code qui vous est fourni, la classe MedImage permet de lire une image et de stocker la donnée sous forme d'un tableau de valeurs d'intensité, la classe Slicer extrait une coupe à travers le volume et la classe Viewer réalise l'affichage d'une coupe.

Affichage de plans X, Y, Z en 3D

1. A partir des classes fournies, développez une interface pour permettre l'affichage de trois plans orthogonaux aux directions X, Y, Z. L'équation du plan sera contrôlée par un curseur permettant à l'utilisateur de sélectionner interactivement le numéro du plan à afficher comme sur la figure suivante:
2. Ajoutez ensuite une fenêtre de visualisation 3D qui permette le repérage des trois plans dans l'espace de la manière suivante: Il vous est possible de créer un objet de type BufferedImage à partir des données contenues dans l'objet MedImage par l'intermédiaire d'un code tel que:

   // création d'un modèle de couleurs: RGB
   int[] nBits = {8, 8, 8}; 
   ComponentColorModel colorModel =
      new ComponentColorModel(ColorSpace.getInstance(ColorSpace.CS_sRGB),
                              nBits, false, false, Transparency.OPAQUE, 0);
   // création d'un raster en écriture de dimension x*y utilisant ce modèle de couleurs
   WritableRaster raster = colorModel.createCompatibleWritableRaster(x, y); 
   // création de la buffered image utilisant ce raster pour stocker les données
   BufferedImage bimg = new BufferedImage(colorModel, raster, false, null); 
   // data = tableau d'octets (R,G,B,R,G,B,R,G,B,R,G,B...) pour chaque pixel de l'image:
   // écrire dans data les données provenant de MedImage
   byte[] data = ((DataBufferByte) raster.getDataBuffer()).getData();
   

3. Implémentez un système de navigation permettant de positionner la caméra sous n'importe quel angle de vue.
4. Une image 3D est souvent anisotrope: la dimension physique d'un voxel n'est pas la même dans toutes les directions. Les méthodes MedImage.vx, MedImage.vy et MedImage.vz retournent la dimension des voxels de l'image dans les trois directions. Utilisez cette information pour corriger le facteur d'anisotropie dans votre image 3D.

Rendu surfacique

Des structures anatomiques représentées par des surfaces peuvent être ajoutées pour enrichir la visualisation de l'image 3D:

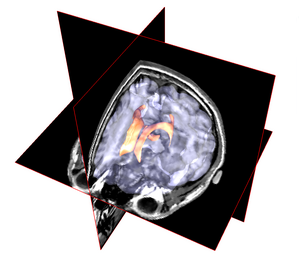
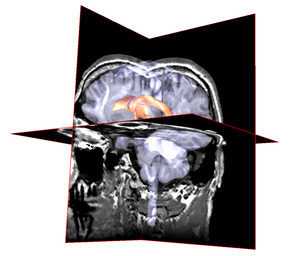
Vous trouverez dans le répertoire de données plusieurs images et maillages de structures anatomique pour l'expérimentation. Les maillages sont composés de polygônes irréguliers (nombre de côtés variables). Les fichiers maillage sont lisible en format texte. Le format de fichier est le suivant:

int                # nombre de sommets
int int int        # position de chaque sommet
...
int int int        # pour chaque sommet, index de ses 3 voisins (définition
...                # des arêtes)
int                # nombre de faces (polygônes)
n i1 i2 ... in     # n = nombre de sommets de chaque polygône
...                # i1 i2 ... in = index des n sommets du polygône

Par exemple, le tétrahèdre représenté dans la figure ci-dessous serait encodé tel que montré à droite.

		4 0.0 0.0 0.0 1.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 1.0 3 2 1 0 2 3 1 0 3 0 1 2 4 3 0 1 2 3 0 1 3 3 0 2 3 3 1 2 3

1. Ajoutez la possibilité de charger et de visualiser des surfaces dans votre scène 3D.
2. Ajoutez un contrôle de transparence permettant de rendre indépendament chaque surface totalement opaque, invisible, ou transparente.
3. Ajoutez un contrôle de couleur de chacune des surfaces.

Textures 3D

Par extension des textures 2D, il est possible de définir une texture 3D. Une texture 3D est un volume d'intensité qu'il est possible de couper par un plan quelconque pour en visualiser une tranche. Imaginez une texture 3D représentant du bois: elle ne contiendrait pas uniquement une image de la surface mais une information sur chaque point du matériau. Plaquer un plan de cette texture 3D reviendrait à couper le volume de bois à la scie et à en visualiser la tranche découpée.

Les images médicales 3D correspondent exactement à des textures 3D: ce sont des volumes denses donnant une information sur l'intensité de chaque point du corps. Extraire un plan de texture 3D dans une image médicale est une manière élégante de visualiser une coupe. On peut alors très simplement extraire n'importe quel plan orthogonal à l'axe des X, Y ou Z mais encore n'importe quel autre plan comme l'illuste la figure suivante:

1. Proposez un paramétrage permettant de contrôler l'orientation d'un plan dans une direction quelconque de l'espace.
2. Ajoutez dans votre interface des contrôles correspondant à ces paramètres.
3. Affichez, en superposition de l'image, le contour du plan défini interactivement par ces contrôles.
4. Créez une texture 3D à partir de l'image médicale.
5. Utilisez le plaquage de texture 3D pour dessiner le contenu du plan d'intersection avec le volume.

Comme pour les textures 2D, les dimensions des textures 3D doivent être des puissances de 2. En outre, en raison de limitation de l'espace de mémoire de texture disponible, une dimension ne peut pas dépasser 128 (une fois la limite dépassée, la texture n'est pas chargée en mémoire et le plan de coupe apparaît blanc). Il faudra donc prévoir de modifier les images (troncature ou redimensionnement) pour qu'elles puissent être chargées en mémoire de texture.

Rendu volumique

Une technique alternative pour la visualisation des images 3D est le rendu volumique. Le rendu volumiqe consiste à estimer que tous les voxels de l'image sont plus ou moins translucides et que le volume est vu en transparence. On apréhende ainsi l'intégralité du volume à travers une seule image que l'on peut faire évoluer en faisant varier l'angle de visualisation.

La méthode la plus directe pour implémenter le rendu volumique consiste à réaliser un lancer de rayon (ray tracing): des rayons sont lancés depuis le point focal de l'oeil virtuel vers tous les voxels de l'image. L'absorbtion/réflexion des rayons est calculée en fonction de la transparence/opacité des voxels rencontrés. On détermine ainsi la couleur de chaque pixel de l'image. Cette méthode est cependant coûteuse en calcul.

Une méthode plus simple de mise en oeuvre et permettant l'utilisation du matériel graphique est le découpage de la scène en plan parallèles entre eux, tous orthogonaux à l'axe de visualisation comme illustrés dans la figure suivante:

Les voxels de chaque plan sont rendus plus ou moins opaques. La superposition de toutes ces couches transparentes donne un apperçu de rendu volumique. Afin d'améliorer la visualisation, il faut encore définir la fonction de transformation des intensité en transparence: on peut privilégier les régions claires en attribuant pour transparence l'intensité de chaque point (les points noirs deviennent complètement transparent et les points blancs complètement opaques). On peut encore spécifier une fonction de correspondance entre intensité et opacité permettant de contrôler les structures visibles. Ainsi, dans les images du cerveau qui vous sont fournies, rendre les intensités de l'image correspondant au crâne, à la matière grise ou à la matière blanche plus ou moins opaques permettent de visualiser ces différentes structures.

1. Modifiez votre programme pour dessiner le contour de votre plan de coupe de manière à ce que celui-ci soit toujours orthogonal à la direction du regard.
2. Dessinez plusieurs plans de coupes en superposition.
3. Attribuez une transparence à chaque intensité de l'image et faîtes afficher le contenu des plans de coupe.