Enoncé itératif

Objectifs du TD : apprendre à répéter plusieurs fois des blocs d'instructions

Dans le chapitre précédent, nous avons vu comment exécuter les blocs d'instructions en tenant compte de certaines conditions grâce à l'énoncé conditionnel if . Nous allons maintenant voir comment répéter l'exécution d'un bloc tant qu'une condition est vérifiée.

EXERCICES DE COURS

1. Enoncé itératif while

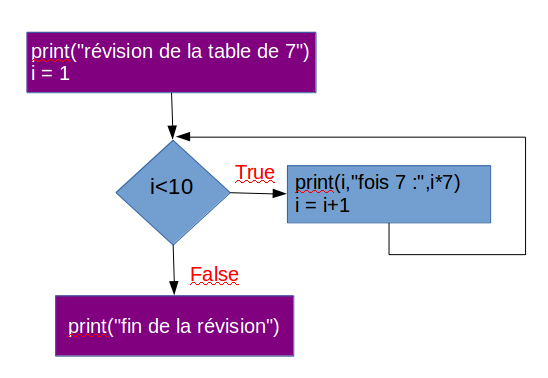
Vous avez sûrement pris l'habitude de créer un nouveau répertoire td3 dans le répertoire algoProgPeiP1. Pour ceux qui ont oublié, faites-le. Lancez idle, ouvrez un nouveau fichier et copiez le programme suivant :

# table de multiplication par 7
print("révision de la table de 7")
i = 1
while i<=10 :
    print(i,"fois 7 :",i*7)
    i = i+1
print("fin de la révision")

Explications : Enoncé itératif while

L'énoncé

   while condition :
      bloc_à_répéter
   bloc_final

où condition est une expression booléenne et bloc_à_répéter et bloc_final sont des blocs d'instructions, est un énoncé itératif (que l'on appelle aussi une boucle puisque l'on revient toujours sur la première instruction du bloc à répéter). Tant que condition s'évalue à True alors bloc_à_répéter est exécuté. Dès que condition vaut False, alors bloc_final est exécuté.
Bien sûr, les énoncés while peuvent être imbriqués c'est à dire que bloc_à_répéter peut lui-même contenir un énoncé while (et aussi des énoncés if).

Pour que l'exécution d'un énoncé itératif termine, il faut que la boucle contienne ce que l'on appelle un variant c'est à dire une variable qui varie et qui assure que la condition pour répéter la boucle va devenir fausse. Dans le programme ci-dessus, l'instruction i = i+1 est un variant : cela fait varier i en partant de sa valeur initiale 1 et en ajoutant 1 à chaque itération de la boucle. Ainsi, la valeur de i croît et l'on est sûr que la condition de répétition de la boucle va devenir fausse (i.e. i devient plus grand que 10).

Exercices

Reprenez le programme de la table de multiplication par 7 et enlever l'instruction i = i+1. Que se passe-t-il ?

Modifiez le programme de la table de multiplication par 7 pour qu'il soit plus général. Pour cela, utilisez la fonction input pour demander à l'utilisateur quelle table de multiplication il veut réviser, et jusqu'à quelle valeur il veut aller. Le résultat de l'exécution de votre programme doit être le suivant :
```
Quelle table voulez-vous réviser ? 3
Jusqu'à quelle valeur ? 12
Révision de la table de 3 jusqu'à 12
1 fois 3  : 3
2 fois 3  : 6
3 fois 3  : 9
4 fois 3  : 12
5 fois 3  : 15
6 fois 3  : 18
7 fois 3  : 21
8 fois 3  : 24
9 fois 3  : 27
10 fois 3  : 30
11 fois 3  : 33
12 fois 3  : 36
fin de la révision
```

Ecrire un programme qui affiche tous les nombres pairs compris entre des valeurs min et max fournies par l'utilisateur.

Ecrire un programme qui lit un entier n et calcule la factorielle de cet entier c'est à dire la multiplication de tous les entiers compris entre 1 et n. Tester votre programme pour des petites valeurs comme 4 ou 6 pour vérifier qu'il est correct. Tester votre programme pour 1000 et 10000. Que se passe-t-il ?

Explications
En Python, les entiers manipulés sont des grands entiers (appelés aussi bignum). Le principe est le suivant. Tant que le calcul effectué tient sur un entier codable sur votre machine (i.e. sur 32 ou 64 bits), Python utilise directement l'opération fournie par l'unité centrale. Par contre, dès que les calculs dépassent la taille machine, l'interprète Python gère lui-même les calculs en décomposant les opérations sur les grands nombres en appels successifs aux opérateurs de l'unité centrale (en gérant par exemple la retenue). Du coup, la taille des opérations est seuleument limitée par la taille de la mémoire vive de votre machine.
D'autres langages comme C ou Java, utilisent directement l'opérateur de l'unité centrale, et ne peuvent pas calculer la factorielle d'un nombre trop grand (en Java, sur une machine 64 bits, on ne peut pas dépasser 31 !).

Reprendre votre programme "initiales.py" (feuille 1) où vous dessinez un rectangle avec vos initiales. La nouvelle version de votre programme lit les initiales, et lit la largeur et la hauteur de votre rectangle (supposée supérieure à 3) et utilise une boucle while.

2. Un peu de dessin avec la tortue

©Céline Auzias

Le module turtle de Python offre la possibilité de faire des dessins à l'aide d'une tortue. L'idée est que la tortue fait des mouvements (avance, recule, tourne, ...) et qu'elle laisse des traces (i.e. on peut imaginer que la queue de la tortue est un pinceau qui laisse une trace sur le sol). Ce module est inspiré du langage de programmation Logo (voir http://fr.wikipedia.org/wiki/Logo_%28langage%29). Les actions élémentaires de la tortue sont (© explications de "Apprendre à programmer avec Python 3" de Gérard Swinnen):

reset()                  On efface tout et on recommence
goto(x, y)               Aller à l'endroit de coordonnées x, y
forward(distance)        Avancer d'une distance donnée
backward(distance)       Reculer
up()                     Relever le crayon (pour pouvoir avancer sans dessiner)
down()                   Abaisser le crayon (pour recommencer à dessiner)
color(couleur)           couleur peut être une chaîne prédéfinie ('red', 'blue', etc.)
left(angle)              Tourner à gauche d'un angle donné (exprimé en degrés)
right(angle)             Tourner à droite
width(épaisseur)         Choisir l'épaisseur du tracé
begin_fill() end_fill()  Remplir un contour fermé à l'aide de la couleur sélectionnée
write(texte)             texte doit être une chaîne de caractères

Pour vous familiariser avec la tortue, tapez le code suivant (il se passe d'explications, regardez simplement le résultat qui a été dessiné) :

# on importe le module turtle 
from turtle import *

# par défaut, la tortue est en (0,0) c'est à dire au milieu
# elle est tournée vers la droite
forward(100)

# suite des déplacements pour faire un carré de côté 100
goto(100,100)
goto(0,100)
#le dernier trait est rouge
color("red")
goto(0,0)

# on écrit un texte
write("J'ai fait un carré")

# maintenant on utilise les angles pour faire un autre carré de largeur 200

up()    # on ne veut pas voir le déplacement pour aller sur 1er angle
	# du carré 
goto(0,120)
down()  # on baisse le pinceau pour recommencer à écrire
# on écrit le premier côté en vert
color("green")
forward(200)
# on tourne à gauche de 90° et on avance de 200 3 fois
left(90)
forward(200)
left(90)
forward(200)
left(90)
forward(200)
write("C'est fini")

Ecrire un programme qui dessine un carré dont la longueur des côtés est fournie par l'utilisateur.

Ecrire un programme qui dessine un triangle équilatéral dont la longueur des côtés est fournie par l'utilisateur.

Ecrire un programme qui dessine un hexagone dont la longueur des côtés est fournie par l'utilisateur.

Remarque

Ecrire un programme qui dessine un escalier qui monte en partant du coin en bas à gauche de la fenêtre. Le nombre de marches, la hauteur et la longueur des marches sont fournies par l'utilisateur. Attention : le dessin de l'escalier ne doit pas sortir de la fenêtre. Ecrivez "départ" en bas de l'escalier. Ecrivez "arrivée" en haut de l'escalier si vous avez pu afficher toutes les marches, ou "tronqué" si vous n'avez pu afficher qu'une partie de l'escalier.
Aide : Pour connaître la taille de la fenêtre dans laquelle se déplace la tortue vous pouvez utiliser :
```
  hauteur = window_height() # récupère la hauteur de la fenêtre
  largeur = window_width()  # récupère la largeur de la fenêtre
```
Puisque le point de coordonnée (0,0) est au milieu de la fenêtre, le point en bas à gauche est en (-largeur/2,-hauteur/2). Il est recommandé de mettre une marge de quelques pixels pour voir la marche du bas.