
|
Détection des collisions dans un moteur 3D temps réel |


Etudiant : |
Guillaume Gourdin |
Organismes : |
4X Technologies ESSI |
Encadreurs : |
4X Technologies : M. Alexandre DelattreM. Johann Liberman ESSI : M. Jean-Claude Lafon |
Intitulé du projet : |
Détection des collisions dans un moteur 3D temps réel. |
Résumé du projet : |
Mon projet consiste à mettre en œuvre des techniques efficaces de détection des collisions dans un monde 3D temps réel. Dans un premier temps, il aura fallu se faire une idée précise de l’état de l’art de ce domaine, en cherchant les algorithmes existants. Puis, à partir de des nombreuses informations récoltées, il faut effectuer une sélection des algorithmes susceptibles de donner de bons résultats après implémentation. Enfin, intervient l’étape de l’implémentation proprement dite, avec des tests dans des environnements réels et validation des choix des algorithmes. |
|
Table des matières |
Chapitre 1 : Présentation du projet
page 31 – Encadrement page 3
2 – Description page 3
3 – Cahier des charges page 4
Chapitre 2 : Evaluation de l’état de l’art
page 51 – Les boites englobantes statiques alignées avec les axes page 5
A – Introduction page 5
B – Construction page 5
C – Détection des collisions page 6
D – Conclusion page 6
2 - Les boites englobantes dynamiques alignées avec les axes page 7
A – Introduction page 7
B – Construction page 7
C – Détection des collisions page 7
D – Conclusion page 7
3 - Les boites englobantes non alignées avec les axes page 8
A – Introduction page 8
B – Construction page 8
C – Détection des collisions page 8
D – Conclusion page 9
4 – La structure d’arbre page 9
A – Introduction page 9
B – Construction page 9
C – Détection des collisions page 9
D – Conclusion page 9
5 – Les arbres BSP page 10
A – Introduction page 10
B – Construction page 10
C – Conclusion page 10
6 – La décimation page 11
A – Introduction page 11
B – Description de l’algorithme page 11
C – Détection des collisions page 11
D – Conclusion page 11
Chapitre 3 : Implémentation
page 121 – Présentation du moteur X3D page 12
A – Présentation générale page 12
B – Les différents modes de rendu page 12
C – Gestion des éléments page 12
2 – Environnement de travail page 13
3 – Les classes C++ page 14
4 – Les boites englobantes alignées avec les axes page 15
5 – Arbre de boites englobantes alignées avec les axes page 16
Chapitre 4 : Planning
page 17Conclusion
page 18Bibliographie
page 19Annexes
page 20
|
Chapitre 1 : Présentation du projet |
|
1 – Contexte |
4X Technologies est une entreprise parisienne spécialisée dans le développement de technologies haut de gamme orientées vers le jeu vidéo. Ses produits phares sont :
Mon projet porte plus spécifiquement sur le moteur X3D. Ce dernier est présent dans les jeux suivants :
|
2 – Description du projet |
Le sujet de mon projet a été proposé par 4X Technologies : il s’agit d’implémenter une détection efficace des collisions dans le moteur 3D temps réel X3D. En effet, il faut savoir que la principale application du moteur X3D est le jeu vidéo. Or, les jeux vidéos en 3D ont besoin d’une gestion efficace des collisions : un personnage ne doit pas passer à travers les murs, une voiture ne doit pas interpénétrer une autre voiture, etc.
Le projet s’est déroulé à l’ESSI, sous l’encadrement de M. Lafon, mais il y a eu également une étroite collaboration avec 4X Technologies, grâce à l’envoi de rapports intermédiaires et de sources de programme via Internet. Je me suis par ailleurs rendu chez 4X Technologies à Paris pendant la semaine de février consacrée au projet afin de préciser l’orientation à donner au projet, mais également pour me procurer le moteur X3D afin de pouvoir travailler à l’ESSI.
|
3 – Cahier des charges |
Le problème de la détection de collisions entre objets en 3 dimensions est loin d’être évident et est encore ouvert car le cahier des charges d’un tel problème contient deux contraintes opposées :
Tout le problème consiste donc à trouver le meilleur compromis coût/précision. Par ailleurs, le moteur X3D est un moteur 3D générique et il faut donc exclure les algorithmes qui s’appuient sur un contexte précis.
X3D possède déjà une détection des collisions. Mais celle-ci est insatisfaisante car trop coûteuse. En effet, elle est basée sur la subdivision de la scène en objets. On teste pour chaque objet s'il y a collision avec la sphère englobante de l'objet, puis s'il y a collision (ce qui arrive souvent), on teste toutes ses faces une par une. Le problème est que certains objets peuvent avoir des centaines de faces. De plus, la recherche des faces en collision passe pour chaque face par un calcul exact du point de collision (ce qui reste relativement coûteux s'il y a beaucoup de faces candidates).
|
Chapitre 2 : Evaluation de l’état de l’art |
Un objet en 3 dimensions est composé, pour X3D comme pour les moteurs 3D courants, de plusieurs faces polygonales. Tester les collisions directement sur ces faces est hors de question pour un moteur temps réel car le coût serait bien trop élevé. Aussi, j’ai effectué des recherches bibliographiques afin de connaître les algorithmes qui permettent aujourd’hui de détecter les collisions sous la contrainte du temps réel. J’ai retenu les algorithmes suivants :
|
1 – Les boites englobantes statiques alignées avec les axes |
A – Introduction
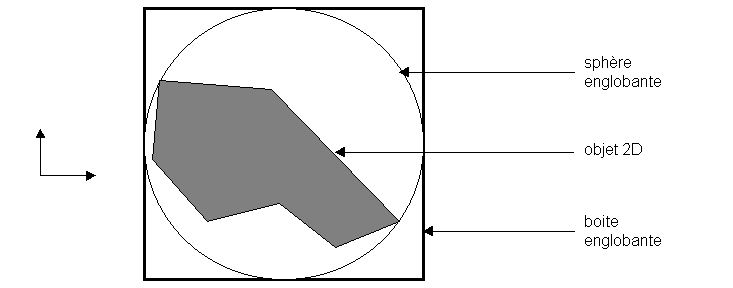
Cette méthode est la plus grossière de toutes. Elle est par conséquent la moins coûteuse en temps machine. Elle consiste à approximer un objet 3D par un cube l’englobant et à tester les collisions sur ces cubes en lieu et place des objets originaux.
B- Construction
Il suffit de déterminer la boite englobante de la sphère englobante de l’objet 3D.
Construction de la sphère englobante d’un objet 3D :
Il suffit de déterminer les points de l’objet les plus éloignés entre eux. Ces points constitueront les extrémités du diamètre de la sphère englobante.
Construction de la boite englobante :
La boite englobante est donc un cube dont les faces sont parallèles aux axes dont on connaît les coordonnées du centre ainsi que la distance séparant les faces du centre. Il est donc aisé d’en déduire les coordonnées des sommets.
C – Détection des collisions
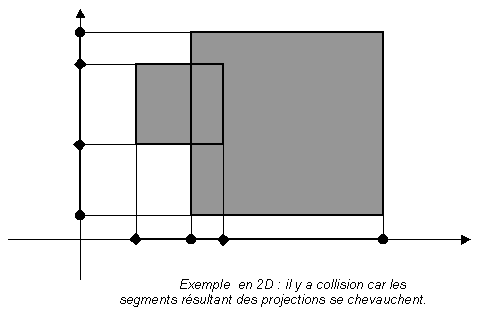
La détection des collisions est alors très simple. En effet, on teste les collisions sur des cubes dont les faces sont parallèles aux axes. Il suffit alors de projeter les faces sur chacun des trois axes X, Y et Z et des tester si les projections se chevauchent ou pas.
D – Conclusion
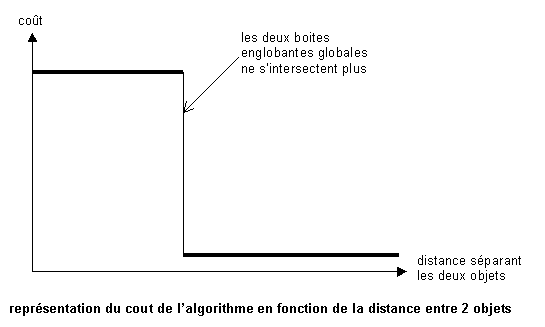
Comme on s’en doute, cette méthode est très grossière et ne répond pas du tout à la contrainte de la précision de la collision. En effet, une collision peut être détectée sur les boites englobantes alors que les objets qu’elles englobent ne se rencontrent pas, particulièrement lorsque les objets sont très allongés
Mais d’un autre côté, c’est la plus performante : la boîte est construite une fois pour toutes et les tests de collisions sont très peu coûteux.
|
2 – Les boites englobantes dynamiques alignées avec les axes |
A – Introduction
Cette méthode est similaire à la méthode précédente, mais elle est un peu plus fine. En effet, on s’affranchit de la contrainte d’une boite statique. Le problème qui survient alors, c’est qu’il faut redimensionner la boite dès que l’objet 3D tournera, d’où des calculs supplémentaires à effectuer en cours d’exécution du programme.
B- Construction
La construction est très aisée : en effet, il suffit de parcourir les coordonnées des sommets, et d’assigner comme sommets de la boîte englobante les min. et max. des coordonnées en X, Y et Z.
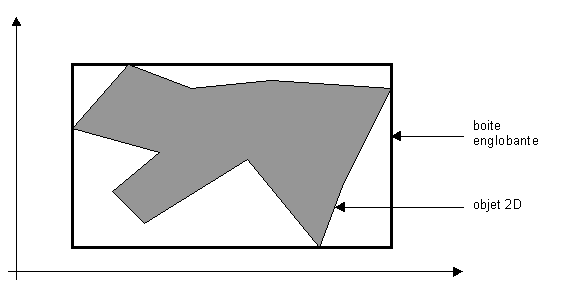
C – Détection des collisions
La détection des collisions s’effectue de la même manière que pour les boites englobantes statiques.
D – Conclusion
Cette méthode efface un peu les défauts de la méthode des boites englobantes statiques, mais ça n’est toujours pas la panacée, la boite, même si ce n’est plus un cube, est toujours une approximation médiocre d’un objet 3D quelconque. Par contre, le peu de calculs supplémentaires qu’elle induit lors de l’exécution sont toujours minimes (car si l’objet ne tourne pas, la boite demeure inchangée) et cette méthode peut être considérée comme très performante.
|
3 – Les boites englobantes non alignées avec les axes |
A – Introduction
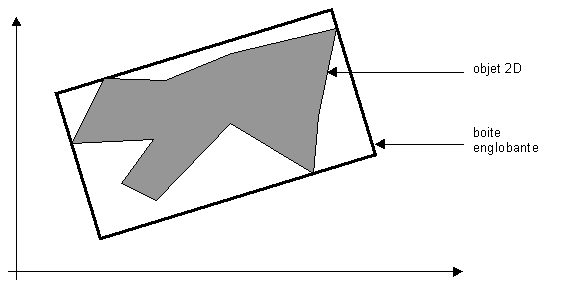
On s’affranchit d’une contrainte supplémentaire : celle des faces des boites devant être parallèles aux axes. On cherche alors à contenir l’objet dans une boite quelconque. Cette méthode permet de construire la boite une unique fois à l’initialisation du programme, mais en revanche, les tests concernant la détection des collisions s’en retrouvent plus ardus.
B- Construction
Dans un premier temps, on détermine le centre de gravité (le barycentre) de l’objet 3D, puis on construit la matrice de covariance de l’ensemble de ces points (pour les détails des calculs, se référer à la bibliographie). Cette matrice étant symétrique, ses vecteurs propres forment une base de R3. La boite englobante aura alors ses faces parallèles à ces axes.
Une amélioration possible de cet algorithme afin de tenir compte de l’éventuelle non-homogénéité des objets 3D est de pondérer lors du calcul du barycentre les points de l’objet par la taille de la facette qu’ils déterminent.
C – Détection des collisions
La détection des collisions s’appuie sur le fait que si deux boites de l’espace sont disjointes, il existe un plan séparant les deux objets, ce plan étant parallèle à une face d’un des deux objets ou à une arête de chaque objet (soit au total 15 tests potentiels : 3 faces pour la première boite, 3 autres pour la seconde, et 9 pour les combinaisons d’arêtes).
Pour vérifier si un tel plan sépare bien deux objets, il faut projeter les boites sur un axe orthogonal au plan séparateur et vérifier si les projections se chevauchent ou pas.
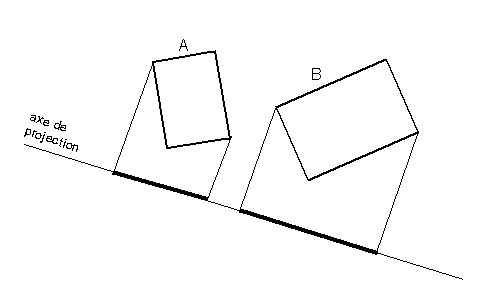
D – Conclusion
Cette méthode est certainement intéressante à implémenter car on évite le problème d’avoir à reconstruire la boite au cours de l’exécution du programme, sauf si l’objet en question se déforme (par exemple un personnage qui bouge). En revanche, les tests de collisions sont très peu coûteux puisque basés sur la projection qui utilise abondamment les produits scalaires qui sont codés en assembleur dans X3D et qui sont donc fortement optimisés.
|
4 – La structure d’arbre |
A – Introduction
Une manière élégante d’optimiser les trois algorithmes suscités est d’utiliser la structure d’arbre.
B – Construction
On construit tout d’abord la boite comme indiqué dans les paragraphes ci-dessus, et on considère que cette boite est la racine de notre arbre. On scinde la boite en deux selon un plan proprement choisi. Le plan sépare également l’objet 3D en deux, et on reconstruit une boite pour chacun des deux sous-objets.
On poursuit le processus jusqu’à ce que l’on estime que la profondeur de l’arbre est suffisante pour une détection précise, on peut également construire l’arbre jusqu’à ce que les sous-objets ne soient que les facettes de l’objet original.
C – Détection des collisions
Si on dispose ainsi de deux arbres, comment tester les collisions ? Il faut tout d’abord considérer les racines des deux arbres (qui sont donc des boites). Si elles ne se rencontrent pas, il n’y a pas de collision. Dans le cas contraire, il faut parcourir les arbres. Une manière de procéder est la suivante : on détermine quelles sont les feuilles du premier arbre qui sont en collision avec la racine du deuxième arbre, et ensuite on teste si ces feuilles chevauchent des feuilles du second arbre. Si c’est le cas, il y a collision.
D – Conclusion
Cette structure d’arbre est très intéressante car elle optimise la précision de la détection de la collision tout en alourdissant raisonnablement les calculs. De plus, il est possible de moduler la précision de la détection en choisissant une profondeur d’arbre plus ou moins grande. Enfin, il est possible d’optimiser le choix du plan de scission en fonction du contexte. Idem pour le parcours de l’arbre.
|
5 – Les arbres BSP |
A – Introduction
Les arbres BSP s’appuient sur le fait qu’il est inutile de tester les collisions entre deux objets s’ils sont éloignés l’un de l’autre. Une manière de faire pourrait être de partionner l’espace selon une grille et de tester les collisions entre deux objets uniquement s’ils appartiennent à la même case de la grille. Les arbres BSP reposent sur ce même principe de partitionnement de l’espace, mais ce dernier est effectué de manière plus intelligente.
B – Construction
Les nœuds d’un arbre BSP sont des hyperplans orientés et les feuilles sont elles des sous parties de l’espace de la scène.
Le mieux est encore de construire un exemple en dimension 2 : on dispose alors de segments orientés. On choisit un segment comme étant la racine de l’arbre, l’espace est alors partitionné en 2 par la droite passant par le segment, et on place chacun des deux sous-espaces dans l’une ou l’autre des 2 feuilles selon que le sous espace est devant ou derrière la droite.
On recommence alors le processus jusqu’à avoir atteint une profondeur d’arbres estimée suffisante ou jusqu’à ce que tous les segments soient dans un nœud. Si un segment est des deux côtés d’un nœud, on le coupe en deux.
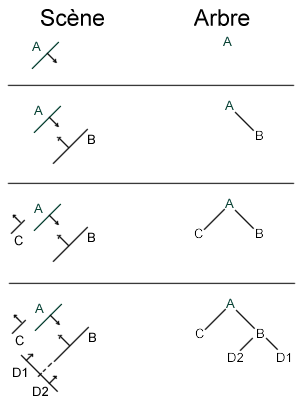
C – Conclusion
Cet algorithme n’est pas à proprement parlé un algorithme de détection de collision. Il permet juste de trier les objets ou les faces proches les uns des autres et donc susceptibles de rentrer en collision.
En fait, je pense que cet algorithme est surtout utile pour détecter la collision d’une caméra avec des murs (comme par exemple dans les jeux), mais il l’est certainement moins pour détecter les collisions dans un monde très dynamique où de nombreux objets bougent car l’intérêt des arbres BSP est qu’ils peuvent être pré-calculés à l’initialisation.
|
6 – La décimation |
A – Introduction
La décimation consiste à enlever à un objet 3D ses sommets les moins significatifs, ce qui permet d’obtenir un objet d’allure semblable à l’objet original, tout en ayant considérablement réduit sa complexité, afin d’effectuer moins de calculs lors de la détection de collisions. En fait, on passe outre la dernière contrainte des algorithmes basés sur les boites englobantes qui stipulait que l’approximation d’un objet 3D devait être une boite.
B- Description de l’algorithme
La décimation consiste à assigner un poids à chaque sommet de l’objet : plus le sommet est significatif, plus le poids sera important. Il suffit alors d’éliminer les sommets dont les poids sont les moins importants, en prenant soin de bien recalculer les poids des sommets après élimination d’un sommet.
Assignation d’un poids :
Il existe plusieurs manière d’assigner un poids à un sommet. L’idée étant que plus le gradient est important, plus le poids sera élevé, c’est-à-dire que plus un sommet est pointu, plus le poids sera élevé. On peut de plus pondérer cette information par le fait que le sommet est proche ou non de ses voisins, qu’il a un nombre élevé de voisins, etc.
Elimination du sommet :
En réalité, on ne supprime pas purement et simplement un sommet, on le fusionne avec un de ses voisins, de telle sorte que le résultat obtenu soit le plus proche de l’objet original.
Une méthode pour choisir le meilleur voisin avec qui fusionner consiste à calculer le maximum ravant des " rondeurs " (c’est-à-dire le rapport de la longueur de l’arête la plus longue sur le rayon du cercle inscrit) des triangles dont le sommet fait partie. Ensuite on calcule le maximum raprès des rondeurs après fusion du sommet avec un de ses voisins. Si raprès > ravant, on autorise la fusion.
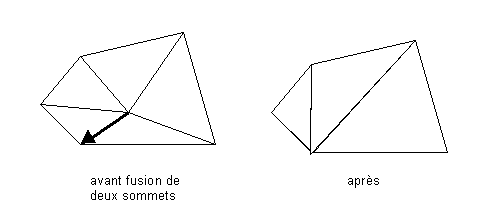
C – Détection des collisions
La détection entre deux objets 3D s’effectue alors en testant si les faces des objets décimés s’intersectent.
D – Conclusion
Cet algorithme peut se révéler intéressant car il est modulable (ou peut régler le taux de décimation) et si les critères de suppression de sommets sont bien choisis, un objet décimé sera très proche de l’objet original, mais comprendra un nombre bien moindre de faces. Par contre, il ne permet pas d’utiliser la structure d’arbre.
|
Chapitre 3 : Implémentation |
|
1 – Présentation du moteur X3D |
A – Présentation générale
Le moteur X3D fonctionne sur un modèle de scènes. Le principe est d’avoir un ensemble d’objets, animations, caméra et lumières chargés dans une scène, puis de faire un rendu de cette scène.
Pour créer une scène, il faut créer les différents éléments qui la composent en utilisant le modeleur 3D Studio Max. Puis, on charge les éléments dans le moteur à partir du fichier 3D Studio où sont décrits les objets, le fichier devant néanmoins auparavant être converti pour qu’il soit lisible par X3D. L’avantage de cette méthode est qu’on utilise toute la puissance de modélisation de 3D Studio.
Le moteur est composé d’une couche haut niveau, et d’une couche bas niveau. La couche haut niveau se charge de gérer l’API du moteur et effectue les opérations de traitements des objets, des animations, des lumières et des caméras. Elle charge pour cela une seconde couche de haut niveau qui effectue entre autres les calculs mathématiques et qui est optimisée pour exploiter les caractéristiques du processeur hôte. Le moteur charge ensuite pour chaque scène une couche de bas niveau effectuant le rendu des scènes.
B – Les différents modes de rendu
Les couches de bas niveau actuellement disponibles sont les suivantes :
Direct3D : Cette couche permet d’effectuer un rendu (logiciel et matériel) grâce à l’API Direct3D de Microsoft. Elle permet ainsi d’exploiter la puissance de toutes les cartes 3D du marché.
Pseudo-scanline : Cette couche permet d’effectuer un rendu logiciel en évitant un maximum les bugs de faces et de recouvrements.
Painter " front to back " : Cette couche permet d’effectuer un rendu logiciel en peintre, mais en évitant les recouvrements.
Enfin, il existe des couches permettant le rendu matériel sur 3DFX, Power VR et les cartes compatibles OpenGL.
C – Gestion des éléments
La gestion des éléments au sein du moteur s’effectue de la manière suivante :
Il existe d’autres type de données (concernant les lumières, le texturage, les caméras, etc.), mais ils n’interviennent pas directement dans la détection de collisions.
|
2 – Environnement de travail |
Le travail de programmation s’effectue sous Windows (sous ses diverses variantes : Windows95, Windows98, Windows 2000 et Windows NT), avec, si possible, DirectX7 installé, afin de jouir de l’accélération matérielle des cartes 3D du marche.
Le langage de programmation est quant à lui le C/C++, l’environnement de programmation étant Microsoft Visual C++ version 6, l’outil standard de développement d’applications Windows.
Enfin, pour tester mes algorithmes, 4X Technologies m’a fourni une scène, dans laquelle se situe une petit boule (composée de 128 faces). Les tests de collisions ont lieu sur cette petite boule, que l’on peut déplacer dans la scène à l’aide des touches du clavier numérique. La scène contient également un plan (1 face), une boîte (6 faces), 2 cônes (126 et 128 faces) et une théière (166 faces).

Apperçu de la scène.
|
3 – Les classes C++ |
Par commodité plus que par nécessité, j’ai choisi de programmer en C++ en utilisant les classes. En effet, l’utilisation des classes permet une plus grande lisibilité et une plus grande réutilisabilité du code. En particulier, j’ai créé les classes suivantes :
BoundingBox : Représente la boite englobante d’un objet en 3 dimensions. Il s’agit donc en réalité d’un parallélépipède. Les six champs de cette classe sont les coordonnées réelles minimales et maximales des sommets du parallélépipède.
Cette classe a de nombreuses méthodes, à commencer par des constructeurs qui permettent de construire la boite englobante d’une face ou d’un objet en 3 dimensions. Il y a également un constructeur par copie qui permet de construire une boite englobante identique à une autre.
Il y a de plus deux méthodes
GetSommetMin(float *x, float *y, float *z) et GetSommetMax(float *x, float *y, float *z), qui, comme leurs noms le laissent subodorer, permettent d’accéder aux coordonnées minimales et maximales de la boite.On dispose également de la méthode
Deplacer(float dx, float dy, float dz) qui permet de déplacer une boite englobante.Enfin, la classe possède la méthode la plus importante :
IsIntersecting(BoundingBox *bBox) qui permet de savoir si une boite englobante en intersecte une autre.
Point3D : Représente un point dans l’espace avec trois coordonnées
x, y et z. La seule méthode de cette classe (excepté le constructeur et le destructeur) est la méthode EstDansBBox(BoundingBox *b)qui renvoie vrai ou faux selon que le point est dans la BoundingBox passée en paramètre ou non.
Face : X3D possède déjà une structure FACE, mais, pour étendre ses fonctionnalités et pour mieux comprendre son fonctionnement, j’ai créé ma propre classe représentant une face. Cette classe est une classe fille de la classe CObArray, qui est une classe standard de Visual C++ et qui permet de construire des tableaux dynamiques. Ainsi, une face est un tableau de Point3D.
On construit une face en ajoutant donc les points qui la compose. Pour ce faire on appelle la méthode
AjouterPoint(Point3D *pt).La classes Face dispose également d’une méthode
EstDansBBox(BoundingBox *b) qui permet de savoir si une face est dans une boite englobante.
Objet3D : De la même manière que pour la classe Face, cette classe a été créée pour étendre les fonctionnalités de la structure OBJECT de X3D. Ses champs sont les suivants :
Nom
: une chaîne de caractère permettant d’identifier l’objet.bBoxGlobale
: la boite englobante globale de l’objet.tableauFaces
: un tableau contenant les faces de l’objet.objetOriginal
: un pointeur vers l’objet original de type OBJECT.Cette classe dispose d’un constructeur initialisant correctement ces différents champs.
Elle possède de plus une méthode permettant de déplacer l’objet et une autre méthode permettant de savoir si un objet en intersecte un autre.
|
4 – Boites englobantes alignées avec les axes |
La première implémentation de détection de collisions aura été basée sur les boites englobantes. Pour ce faire, j’ai étendu la classe Objet3D décrite ci-dessus en lui ajoutant en tableau de boites englobantes de faces, c’est-à-dire que l’on créé pour chaque face sa boite englobante que l’on mémorise en l’insérant dans un tableau.
L’algorithme se décompose en deux phases :
Cet algorithme, s’il donne de bons résultats au niveau de la précision, est par contre très mauvais au niveau des performances, puisqu’il est quadratique (on teste toutes les faces d’un objet avec toutes les faces de l’autre objet). Ce défaut est visible à l’œil nu, puisque lorsque deux objets sont proches et qu’il faut effectuer les tests face par face, un ralentissement sensible de l’affichage a lieu. Par exemple, lorsque la boule entre en collisions avec la théière, il y a 21 248 tests d’intersection de boites englobantes qui sont effectués.
Néanmoins, l’implémentation de cette détection m’a permis de me familiariser avec le moteur X3D et avec les structures qui le composent.

Il n’y a pas de collisions détectées,
alors que la boule est proche de la théière.
|
5 – Arbre de boites englobantes alignées avec les axes |
Ensuite, conformément aux recommandations de mes encadreurs, j’ai codé la détection basée sur la structure d’arbre décrite au chapitre précédent. En effet, cette méthode était a priori celle susceptible de donner les meilleurs résultats en terme de rapport précision/coût.
Pour ce faire, j’ai implémenté la classe AABBTree qui possède comme champs principaux les deux sous-arbres qui sont donc eux-mêmes de type AABBTree. Il y a également une boite englobante de l’arbre entier, ainsi qu’un tableau de boites englobantes des faces intersectant le plan de partition.
Cette classe possède donc un constructeur, qui permet de construire un arbre récursivement à partir d’un tableau de faces. On procède de la manière suivante : on parcours les faces du tableau passé en paramètre. Si une face intersecte le plan de partition, on ajoute sa boite englobante au champ des boites englobantes (cf. ci-dessus). Si ce n’est pas le cas, on regarde de quel côté du plan de partition se situe la face, et on l’ajoute dans un tableau. On dispose donc après le tri de deux tableaux contenant chacun les faces situées d’un côté ou de l’autre du plan de partition. On construit alors les deux sous arbres avec ces deux tableaux, s’ils ne sont pas vides. Le plan de partition est celui qui coupe en deux la boite englobante de l’arbre entier (il est parallèle tour à tour à xOy, xOz et yOz).
Cet algorithme est particulièrement performant, puisque le tri des faces qu’il induit permet de réduire considérablement le nombre de tests de boites englobantes. En effet, selon la position de la boule, on effectue moins de 250 test ! A comparer avec 21 248 tests de l’algorithme précédent, soit un facteur de réduction du nombre de tests approchant les 100, alors que la précision est toujours la même.
Cet algorithme ne répond pas entièrement aux problèmes de la détection de collisions dans un jeu vidéo, puisque les problèmes d’animations et de déformations d’objets, ainsi que le problème de la discrétisation du mouvement ne sont pas réglés. Pour l’instant, on regarde une scène fixe et on se contente de dire s’il y a des objets en collision. Néanmoins, une étape importante a été franchie. En effet, l’algorithme basé sur la structure d’arbres permet un tri particulièrement efficace des faces, et est beaucoup plus performant que l’algorithme de base inclus dans X3D qui lui est quadratique.

Détection d’une collision.
|
Chapitre 4 : Planning |
Mois de décembre 1999 :
|
1ière semaine |
2ième semaine |
3ième semaine |
4ième semaine |
|
Recherche d’informations bibliographiques |
|||
|
Rédaction du premier rapport intermédiaire |
Rédaction du deuxième rapport intermédiaire |
Rédaction du troisième rapport intermédiaire |
|
Mois de janvier 2000 :
|
1ière semaine |
2ième semaine |
3ième semaine |
4ième semaine |
|
Recherches bibliographiques |
|||
|
Rédaction du quatrième rapport intermédiaire |
|||
Mois de février 2000 :
|
1ière semaine |
2ième semaine |
3ième semaine |
4ième semaine |
|
Recherches bibliographiques |
Voyage à Paris pour me familiariser avec X3D et pour décider avec M. Alexandre Delattre des algorithmes à implanter dans X3D. |
Implémentation de la structure d’arbre avec les boites englobantes dynamiques alignées avec les axes. |
|
|
Rédaction du quatrième rapport intermédiaire |
|||
Mois de mars 2000 :
|
1ière semaine |
2ième semaine |
3ième semaine |
4ième semaine |
|
Implémentation de la structure d’arbre avec les boites englobantes alignées avec les axes. |
|||
Mois d’avril 2000 :
|
1ière semaine |
2ième semaine |
|
Implémentation de la structure d’arbre avec les boites englobantes alignées avec les axes. |
|
|
Rédaction du rapport final. |
|
|
Conclusion |
|
La détection des collisions est aujourd’hui un thème de recherche majeur en informatique. Ses applications dépassent largement le domaine du jeu vidéo et apparaissent également dans les domaine de la CAO et de l’image de synthèse par exemple. A chaque fois, les contraintes sont différentes. Le jeu vidéo impose des algorithmes performants, quitte à sacrifier quelque peu la précision de la détection. En CAO, au contraire, on recherche d’abord des algorithmes extrêmement précis, souvent avec calcul du point d’impact. Enfin, en images de synthèse, se posent d’autres problèmes, comme par exemple la détection d’auto-collisions dans le cadre d’objets déformables (comme des vêtements).
Participer à un domaine où la recherche est bouillonnante est un des aspects positifs de ce projet. En effet, mon projet a nécessité un important travail de recherche et de réflexion préalablement à toute implémentation. La découverte de cette importante phase de réflexion et de discussion qui m’était inconnue a été très bénéfique pour moi.
Un autre aspect positif de ce projet est que le travail de réflexion aboutit sur une implémentation concrète qui sera éventuellement incorporée à un produit commercial. D’ailleurs, le travail de programmation a été lui aussi très intéressant car le code doit être performant, sous peine d’anéantir les optimisations d’un algorithme.
C’est ce juste mariage entre recherche et programmation qui fait à mon avis tout l’attrait de mon projet.
|
Bibliographie |
Article :
Livres :
Boites alignées avec les axes :
Boites non alignées avec les axes :
Arbres BSP :
Décimation :
|
Annexes |
// AABBTree.cpp: implementationde la classe AABBTree.
//
// Un arbre AABB est un arbre de boites parallèles aux axes
//
//////////////////////////////////////////////////////////////////////
//inclusions
#include <afx.h>
#include <afxcoll.h>
#include "project.h"
#include "Face.h"
#include "BoundingBox.h"
#include "Objet3D.h"
#include "AABBTree.h"
//////////////////////////////////////////////////////////////////////
// Construction/Destruction
//////////////////////////////////////////////////////////////////////
AABBTree::AABBTree()
{
}
AABBTree::~AABBTree()
{
for (int i = 0; i < bBoxNoeud->GetSize(); i++)
delete bBoxNoeud->GetAt(i);
delete this->bBoxNoeud;
delete this->bBox;
if (this->sousArbreDroit != NULL)
delete this->sousArbreDroit;
if (this->sousArbreGauche != NULL)
delete this->sousArbreGauche;
}
//////////////////////////////////////////////////////////////////////
//Construit un arbre AABB
//
// paramètres:
// -tableauDeFaces: le tableau contenant les faces dont on
// souhaite construire l'arbre
// -profondeur: la profondeur à laquelle on se situe
// permet dans la recursion de choisir le plan de partition
// -b: la boite englobante de l'objet
//////////////////////////////////////////////////////////////////////
AABBTree::AABBTree(CObArray *tableauDeFaces, int profondeur, BoundingBox *b)
{
BoundingBox *bBoxGauche = new BoundingBox(b);
BoundingBox *bBoxDroite = new BoundingBox(b);
this->bBox = b;
this->bBoxNoeud = new CObArray();
float distance;
//on découpe la boite englobante selon x, y ou z
switch (profondeur %3)
{
case 0:
distance = b->x_max - b->x_min;
bBoxGauche->x_max = b->x_min + distance/2;
bBoxDroite->x_min = b->x_min + distance/2;
break;
case 1:
distance = b->y_max - b->y_min;
bBoxGauche->y_max = b->y_min + distance/2;
bBoxDroite->y_min = b->y_min + distance/2;
break;
case 2:
distance = b->z_max - b->z_min;
bBoxGauche->z_max = b->z_min + distance/2;
bBoxDroite->z_min = b->z_min + distance/2;
break;
}
//on trie les faces selon qu'elles appartiennent à telle ou telle bounding box
//si une face intersecte l'intersection des bounding box, on l'ajoute au noeud
CObArray *tableauFacesGauche = new CObArray();
CObArray *tableauFacesDroite = new CObArray();
Face *faceCourante;
for (int i = 0; i < tableauDeFaces->GetSize(); i++)
{
faceCourante = (Face*)tableauDeFaces->GetAt(i);
if (faceCourante->EstDansBBox(bBoxGauche) == TRUE)
{
tableauFacesGauche->Add(faceCourante);
}
else
{
if (faceCourante->EstDansBBox(bBoxDroite) == TRUE)
tableauFacesDroite->Add(faceCourante);
else
this->bBoxNoeud->Add(new BoundingBox(faceCourante));
}
}
//on fait la récursion
profondeur ++;
if ( (tableauFacesGauche->GetSize() == 0) || (profondeur > 200) )
{
delete bBoxGauche;
this->sousArbreGauche = NULL;
}
else
this->sousArbreGauche = new AABBTree(tableauFacesGauche, profondeur, bBoxGauche);
if ( (tableauFacesDroite->GetSize() == 0) || (profondeur > 200) )
{
delete bBoxDroite;
this->sousArbreDroit = NULL;
}
else
this->sousArbreDroit = new AABBTree(tableauFacesDroite, profondeur, bBoxDroite);
delete tableauFacesDroite;
delete tableauFacesGauche;
}
//////////////////////////////////////////////////////////////////////
// retourne la profondeur d'un arbre
//////////////////////////////////////////////////////////////////////
int AABBTree::GetProfondeur()
{
if (this == NULL)
return 0;
else
{
int profGauche = this->sousArbreGauche->GetProfondeur();
int profDroite = this->sousArbreDroit->GetProfondeur();
int maxProf;
if (profGauche > profDroite)
maxProf = profGauche;
else
maxProf = profDroite;
return 1 + maxProf;
}
}
//////////////////////////////////////////////////////////////////////
//renvoie VRAI si un arbre en intersecte un autre
//////////////////////////////////////////////////////////////////////
BOOL AABBTree::IsIntersecting(AABBTree *arbre)
{
BoundingBox *b1 = this->bBox;
BoundingBox *b2 = arbre->bBox;
//si les boites englobantes globales ne s'intersectent pas,
//on renvoie FAUX
if (b1->IsIntersecting(b2) == false)
return false;
//on récupère les bounding box intersectées
CObArray *tableauIntersectingBBox = new CObArray();
arbre->GetIntersectingBBox(tableauIntersectingBBox, this->bBox);
//on teste si une de ces bounding box intersecte l'arbre
BoundingBox *b;
for (int i = 0; i < tableauIntersectingBBox->GetSize(); i++)
{
b = (BoundingBox*)tableauIntersectingBBox->GetAt(i);
if (this->IsIntersecting(b) == TRUE)
{
//si c'est le cas, on renvoie VRAI
delete tableauIntersectingBBox;
return true;
}
}
delete tableauIntersectingBBox;
//sinon on renvoie FAUX
return false;
}
//////////////////////////////////////////////////////////////////////
//Ajoute dans tableauBBax passé en paramètre les boites englobantes
//situées aux feuilles de l'arbre et intersectant la boite englobante b
//passée en paramètre.
//////////////////////////////////////////////////////////////////////
void AABBTree::GetIntersectingBBox(CObArray *tableauBBox, BoundingBox *b)
{
BoundingBox *bBox;
//on teste d'abord les faces du noeud
for (int i = 0; i < this->bBoxNoeud->GetSize(); i++)
{
bBox = (BoundingBox*)bBoxNoeud->GetAt(i);
nbTests ++;
if (bBox->IsIntersecting(b) == TRUE)
tableauBBox->Add(bBox);
}
//et on fait la recursion
if ( (this->sousArbreDroit != NULL) && (this->sousArbreDroit->bBox->IsIntersecting(b) == TRUE) )
sousArbreDroit->GetIntersectingBBox(tableauBBox, b);
if ( (this->sousArbreGauche != NULL) && (this->sousArbreGauche->bBox->IsIntersecting(b) == TRUE) )
sousArbreGauche->GetIntersectingBBox(tableauBBox, b);
}
//////////////////////////////////////////////////////////////////////
//Déplace un arbre.
//////////////////////////////////////////////////////////////////////
void AABBTree::Deplacer(float dx, float dy, float dz)
{
//on déplace la boite englobante globale
this->bBox->Deplacer(dx, dy, dz);
//et les boites englobantes du noeud
BoundingBox *b;
for (int i = 0; i < this->bBoxNoeud->GetSize(); i++)
{
b = (BoundingBox*)this->bBoxNoeud->GetAt(i);
b->Deplacer(dx, dy, dz);
}
//et on fait la recursion
if (this->sousArbreDroit != NULL)
this->sousArbreDroit->Deplacer(dx, dy, dz);
if (this->sousArbreGauche != NULL)
this->sousArbreGauche->Deplacer(dx, dy, dz);
}
//////////////////////////////////////////////////////////////////////
//Renvoie VRAI si l'arbre intersecte la boite englobante b
//passée en paramètre.
//////////////////////////////////////////////////////////////////////
bool AABBTree::IsIntersecting(BoundingBox *b)
{
//on teste les boites englobantes du noeud
BoundingBox *bBox;
for (int i = 0; i < this->bBoxNoeud->GetSize(); i++)
{
bBox = (BoundingBox*)this->bBoxNoeud->GetAt(i);
nbTests++;
if (bBox->IsIntersecting(b) == TRUE)
return true;
}
//on fait la récursion
bool result1 = false, result2 = false;
if (this->sousArbreGauche != NULL)
result1 = this->sousArbreGauche->IsIntersecting(b);
if (this->sousArbreDroit != NULL)
result2 = this->sousArbreDroit->IsIntersecting(b);
if ( (result1 == true) || (result2 == true) )
return true;
else
return false;
}
// BoudingBox.cpp: implementation de la classe BoudingBox.
//
//////////////////////////////////////////////////////////////////////
#define WIN32_LEAN_AND_MEAN
#define STRICT
#include <afx.h>
#include "project.h"
#include "Face.h"
#include "Point3D.h"
#include "BoundingBox.h"
//////////////////////////////////////////////////////////////////////
// Construction/Destruction
//////////////////////////////////////////////////////////////////////
BoundingBox::BoundingBox()
{
}
//////////////////////////////////////////////////////////////////////
//Création d'une boite englobante à partir de la structure BOX de X3D
//////////////////////////////////////////////////////////////////////
BoundingBox::BoundingBox(BOX *bBox)
{
//min
this->x_min = bBox->V[0].x;
this->y_min = bBox->V[0].y;
this->z_min = bBox->V[0].z;
//on parcours les sommets de bBox
for (int i = 1; i < 8; i++)
{
if (x_min > bBox->V[i].x)
x_min = bBox->V[i].x;
if (y_min > bBox->V[i].y)
y_min = bBox->V[i].y;
if (z_min > bBox->V[i].z)
z_min = bBox->V[i].z;
}
//max
this->x_max = bBox->V[0].x;
this->y_max = bBox->V[0].y;
this->z_max = bBox->V[0].z;
//on parcours les sommets de bBox
for (i = 1; i < 8; i++)
{
if (x_max < bBox->V[i].x)
x_max = bBox->V[i].x;
if (y_max < bBox->V[i].y)
y_max = bBox->V[i].y;
if (z_max < bBox->V[i].z)
z_max = bBox->V[i].z;
}
}
//////////////////////////////////////////////////////////////////////
//Constructeur par copie. Créé une boite englobante identique à
//celle passée en paramètre.
//////////////////////////////////////////////////////////////////////
BoundingBox::BoundingBox(BoundingBox *bBox)
{
this->x_min = bBox->x_min;
this->y_min = bBox->y_min;
this->z_min = bBox->z_min;
this->x_max = bBox->x_max;
this->y_max = bBox->y_max;
this->z_max = bBox->z_max;
}
//////////////////////////////////////////////////////////////////////
//Créé la bounding box d'une face.
//////////////////////////////////////////////////////////////////////
BoundingBox::BoundingBox(Face *f)
{
Point3D *point = (Point3D*)f->GetAt(0);
this->x_min = point->x;
this->y_min = point->y;
this->z_min = point->z;
this->x_max = point->x;
this->y_max = point->y;
this->z_max = point->z;
//on parcourt les points de la face
for (int i = 1; i < f->GetSize(); i++)
{
point = (Point3D*)f->GetAt(i);
if (point->x < this->x_min)
this->x_min = point->x;
if (point->y < this->y_min)
this->y_min = point->y;
if (point->z < this->z_min)
this->z_min = point->z;
if (point->x > this->x_max)
this->x_max = point->x;
if (point->y > this->y_max)
this->y_max = point->y;
if (point->z > this->z_max)
this->z_max = point->z;
}
}
//////////////////////////////////////////////////////////////////////
//Création de la BoundingBox de la ième face d'un objet
//////////////////////////////////////////////////////////////////////
BoundingBox::BoundingBox(OBJECT *objet, int indexFace)
{
//on récupère la face concernée
FACE *face = objet->Face[indexFace];
//on récupère les valeurs min et max des coordonnées de la face
int indice = face->Pt[0];
VERTEX *v = &objet->Vertex[indice];
float x_min = v->x;
float y_min = v->y;
float z_min = v->z;
float x_max = v->x;
float y_max = v->y;
float z_max = v->z;
//min
for (int i = 0; i < face->Number_Vertex; i++)
{
indice = face->Pt[i];
v = &objet->Vertex[indice];
if (v->x < x_min)
x_min = v->x;
if (v->y < y_min)
y_min = v->y;
if (v->z < z_min)
z_min = v->z;
}
//max
for (i = 0; i < face->Number_Vertex; i++)
{
indice = face->Pt[i];
v = &objet->Vertex[indice];
if (v->x > x_max)
x_max = v->x;
if (v->y > y_max)
y_max = v->y;
if (v->z > z_max)
z_max = v->z;
}
//et assigne les valeurs min et max à this
this->x_min = x_min;
this->y_min = y_min;
this->z_min = z_min;
this->x_max = x_max;
this->y_max = y_max;
this->z_max = z_max;
}
BoundingBox::~BoundingBox()
{
}
//////////////////////////////////////////////////////////////////////
//Renvoie VRAI si la boite englobante intersecte la boite englobante
//passée en paramètre.
//////////////////////////////////////////////////////////////////////
BOOL BoundingBox::IsIntersecting(BoundingBox *bBox)
{
if ( (this->x_min < bBox->x_max) && (bBox->x_min < this->x_max) &&
(this->y_min < bBox->y_max) && (bBox->y_min < this->y_max) &&
(this->z_min < bBox->z_max) && (bBox->z_min < this->z_max) )
return TRUE;
else
return FALSE;
}
//////////////////////////////////////////////////////////////////////
//Déplace une boite englobante.
//////////////////////////////////////////////////////////////////////
void BoundingBox::Deplacer(float dx, float dy, float dz)
{
x_min += dx;
y_min += dy;
z_min += dz;
x_max += dx;
y_max += dy;
z_max += dz;
}
//////////////////////////////////////////////////////////////////////
//Renvoie les coordonnées du sommet min.
//////////////////////////////////////////////////////////////////////
void BoundingBox::GetSommetMin(float *x, float *y, float *z)
{
*x = this->x_min;
*y = this->y_min;
*z = this->z_min;
}
//////////////////////////////////////////////////////////////////////
//Renvoie les coordonnées du sommet max.
//////////////////////////////////////////////////////////////////////
void BoundingBox::GetSommetMax(float *x, float *y, float *z)
{
*x = this->x_max;
*y = this->y_max;
*z = this->z_max;
}