Td4
l'élimination des surfaces cachées. Le Z-buffer. Les BSPs.

L'élimination des surfaces cachées

"c'est facile", nous dit M.Buffa, Le test de visibilité, c'est pour afficher uniquement les facettes qui nous font face.

Pour cela, on calcule les normales de toutes les faces, et on les compare à l'angle de la caméra.
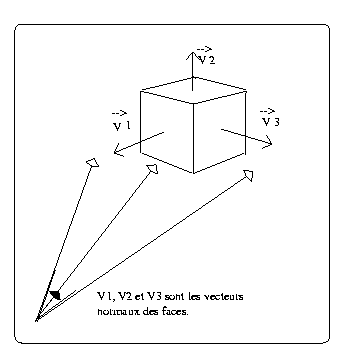
soient v1 et v2, 2 vecteurs de la face incriminée, on calcule le vecteur N normal à la face par :

ensuite, on le norme en le divisant par || v1 || . || v2 ||

V est le vecteur vision (normé lui aussi).

cos ( alpha ) = N . V ,

cos ( alpha ) est compris entre 0 et 1, et cos ( alpha ) est nul, si alpha est nul.

donc si ce produit est nul, la face est face à nous.

L'algorithme du peintre & le Z-Buffer

on peint en commencant par le dessous, et on peint par dessus chaque fois que necessaire. Ainsi, les "couches de peintures" se superposent. D'un coté, ce n'est pas performant, et on perd du temps, et d'un autre, on peut facilement réaliser les superpositions de couleurs, avec de l'apha-transparence. Si la position actuellement représentée à l'endroit ou l'on souhaite afficher un point précede par la distance à la caméra le point qu'on souhaite poser, on laisse ce point. Si la distance est superieure pour l'ancien point, on le remplace. Il est possible à ce moment de sommer les couleurs en fonction du channel alpha.

alpha(couleur courante) + 1 - alpha(couleur precedente)
Dans les autres cas, on affiche normalement la ou il n'y avait rien.

Trucs pour aller plus vite :

Si on fait un tri des faces auparavant (quick sort pour le calcul du Z-buffer), on gagne du temps.

Si on emploie moitié des entiers, et moitié des flottants, on a des chances d'effectuer le calcul plus vite, car les 2 s'effectuent en paralléle.

Pour obtenir plus de précisions, lors des intersections :

Toutes les faces sont balayées par un filtre bilinéaire : c'est à dire par un passage d'abord horizontal et ensuite vertical sur tous les pixels du triangle, afin qu'ils soient projettés sur l'écran (et pas seulement leur centre et leurs coins).

Les BSPs

Attention : Les bsp ne peuvent servir que pour des objets localement fixes.

Voici un exemple en 2D, ensuite on extrudera, et ça se compliquera, parce que les plans (aussi) peuvent se couper.

On numerote les faces par des caractéres alphabétiques, et on les traite l'une aprés l'autre (on les fait rentrer dans l'arbre), par ordre alphabétique. C'est à dire qu'on les découpe en morceaux numérotés si besoin (un segment précédent existe déjà).

A chaque segment qu'on ajoute, on découpe la boite englobante en 2 autres boites englobantes.

Essayez de reconstituer l'arbre ci dessous, à l'aide de la scéne ci contre par ordre alphabétique.

arbre obtenu :

<== à gauche = derriére dans le plan.

      A
     / \
    /   \
   C2    B
  /     / \
 /     /   \
E1    E3    C1
           /
          /
         D
        /
       /
      E2

==> à droite = devant dans le plan.

Parcours de l'arbre : On dessinera dans l'ordre : E1, C2, A, E3, B, C1, E2, D.
(parcours gauche centre droite)

Technique de DOOM sur les BSPs :

Tri inverse, du plus proche, aux plus eloignés :

si le lancer de rayon touche un objet : on trace le point de la couleur désirée.

si le lancer de rayon ne touche rien :

si le z est vers le haut : ciel.
si le z est vers le bas : sol.

Plus on descend profond dans l'arbre, plus la face est loin, plus on a placé le "seuil de visibilité" loin. Les faces lointaines seront plus sombres voir la lumiere.