On effectuera une rotation à la souris, aidé du principe de la boule virtuelle qui est le suivant :
Déroulement à l'intérieur de la zone Déroulement à l'extérieur de la zone
Chaque point de l'objet effectue une rotation par rapport au centre de l'objet, et doit tenir compte uniquement de sa distance avec le centre de l'objet (le rayon du cercle décrit), afin que chaque point de la sphére se déplace à la surface du cercle de façon reguliére (uniforme). C'est pourquoi on normalise les vecteurs. En effet, sur un cercle vu de face, les points les plus éloignés du centre de la sphére vont forcement se déplacer moins vite que les points les plus au centre.

De plus, on doit redonner au vecteur 2D une dimension 3D afin que le mouvement ne souffre pas du phénoméne d'applatissement sur l'écran.
La Rotation

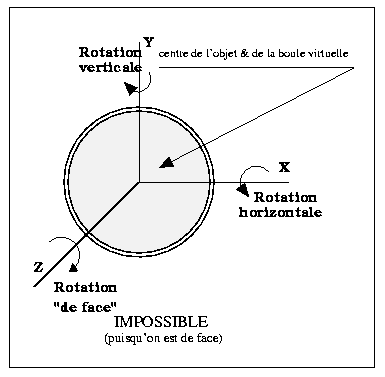
Partie 1 : preparer le terrain

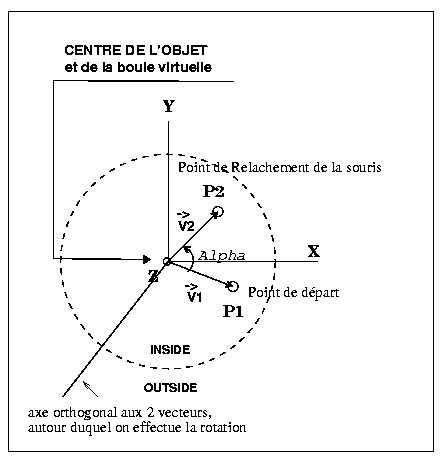
  1. Calculer v->1 à partir de P1 et P1'
  2. Calculer v->2 à partir de P2 et P2'

    • P : position des points (en pixels) à l'instant mouse-pressed.
    • P' : position des points (en pixels) à l'instant mouse-released.
    • X = X1 - X'1.
    • Y = Y1 - Y'1.
    • Z = Z1 - Z'1.
    • à partir de la formule : R2 = X2 + Y2+ Z2, on calcule Z.
      => Z = racine ( R2 - X2 - Y2 )
      (sans oublier de mettre X et Y dans le repere global)
    • v-> = [ X Y Z ]

  3. Calculer le produit vectoriel de V->1 et V->2

    • V->1 ^ V->2 = V->3 = [ X3 Y3 Z3 ]
      avec :
      • X3 = Y1 * Z2 - Z1 * Y2
      • Y3 = Z1 * X2 - X1 * Z2
      • Z3 = X1 * Y2 - Y1 * X2

  4. Calculer le produit scalaire de V->1 et V->2

    • V->1 . V->2 = dotProd = X1 * X2 + Y1 * Y2 + Z1 * Z2

  5. Calculer alpha à partir du produit scalaire.

    • alpha = asin ( V->1 ^ V->2 )
    • alpha = acos ( V->1 . V->2 )

  6. Calculer la matrice de rotation qui correspond à une rotation alpha autour de V->1 ^ V->2 en Y. 
     ---------------------------------------------
|       1        |     0     |  sin ( alpha ) |
|---------------------------------------------|
|       0        |     1     |      0         |
|---------------------------------------------|
| sin ( alpha )  |     0     |      1         |
 ---------------------------------------------
à partir de maintenant, on appellera la matrice obtenue par V->1 ^ V->2 : A->.

Partie 2 : changer l'axe de rotation

La rotation à effectuer ? R(alpha).
autour de quel axe faut-il l'effectuer ? A->.
à quelle rotation correspond cet axe ? la matrice calculée au dessus que nous appelerons Ruvw.
à quelle position ? T-1 par rapport à l'objet.


Donc la nouvelle position de l'objet est : T-1 . Ruvw . R(alpha) . Ruvw-1 . T

Pour que cette rotation soit définitive, on doit transformer :

nouveau LocalToGlobal = LocalToGlobal-1 . Ruvw . LocalToGlobal
et
nouveau GlobalToLocal = GlobalToLocal . Ruvw-1 . GlobalToLocal-1