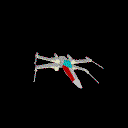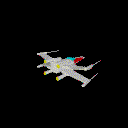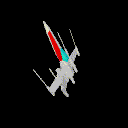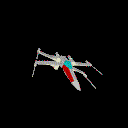TD 4 : élimination des parties cachées
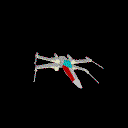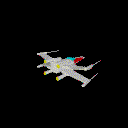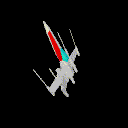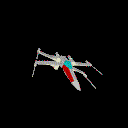
Introduction
Vous allez modifier votre programme pour implémenter deux des algorithmes
étudiés en cours : le test de visibilité et l'algorithme
du peintre (tri des facettes)
Test de visibilité
Ce test utilise la normale de chaque facette de l'objet. Si l'angle entre
cette normale et le vecteur allant d'un point de la facette jusqu'à
la caméra est inférieur à 90 degrés, la face
est visible, sinon elle n'est pas visible.
Voici le test de visibilité en action :
Sans le test de visibilité
Avec le test de visibilité
Pour implémenter cet algorithme, vous allez devoir accomplir
les tâches suivantes
-
Sitôt l'objet lu et son repère centré, vous allez pré-calculer
les normales de chaque faces. Bien entendu, ces normales sont calculées
dans le repère objet et demeureront constantes pendant toute la
durée de vie de l'objet. Ne pas oublier de les normaliser. Je vous
conseille d'écrire une fonction ayant cet entête :
static void precalculeNormales(Object * obj);
-
Au moment du dessin, dans la fonction draw_object, dans la boucle des facettes,
vous allez
-
Transformer la normale à la face courante dans le repère
caméra
-
Calculer le vecteur de visée dans le repère caméra
(il suffit de prendre un sommet quelconque de la facette, puisque le test
de visibilité décide si une facette est entièrement
visible ou entièrement cachée), le normaliser.
-
Calculer le produit scalaire entre la normale dans le repère caméra
et ce vecteur. Si ce produit scalaire est qupérieur à zéro,
la face est visible.
-
Tester sur des objets convexes comme la sphère (ball.obj) ou le
cube (cube_tri.obj).
-
Le produit scalaire étant compris entre 0 et 1 si la face est visible,
il est très facile de simuler un pseudo-éclairage en utilisant
ce produit scalaire. Si vous n'utilisez pas l'option -bw lors du lancement
du programme, la palette de couleurs utilisée est alors une rampe
de 255 niveaux de gris. Le produit scalaire * 255 donne donc une intensité
de lumière comprise entre 0 et 255, proportionelle à l'angle
entre la normale de la face et la direction de vue. Plus l'angle est petit,
plus la face est éclairée.
Remplacez donc l'appel à la fonction DrawFace par un appel à
la fonction FillFace qui affiche une face non pas en fil de fer mais en
couleur pleine, et mettez en dernier paramètre 255 * le produit
scalaire.
En utilisant le produit scalaire entre la normale et la direction
de vue pour simuler lun éclairage de face
Algorithme du peintre
Le test de visibilité permet de séparer l'ensemble des facettes
d'un objet en deux groupes : celles qui sont face à la caméra
et les autres qui sont non visibles. Parmi les facettes visibles, si l'objet
n'est pas convexe, on observe un phénomène de recouvrement
et le rendu final obtenu avec le simple test de visibilité n'est
pas convenable :
X-Wing en tenant compte du seul algorithme de visibilité
L'algorithme du peintre consiste donc à trier les facettes en fonction
de leur distance par rapport à la caméra, puis à les
dessiner dans l'ordre de la plus éloignée à la plus
proche. Si on utilise une fonction de dessin de faces qui remplit les faces
au lieu de les dessiner en fil de fer, on obtient à la fin du dessin
l'illusion des faces cachées :
Le X-Wing avec l'algorithme du peintre
Pour implémenter cet algorithme, vous allez utiliser la fonction
quicksort du C, et un tableau intermédiaire contenant les indices
des faces visibles. Voici l'algorithme (dans draw_object)
-
Déclarer un tableau d'entiers de taille le nombre de faces de l'objet
-
Faire une première boucle sur les faces. Chaque fois qu'une face
est visible (test de visibilté), insérer son indice dans
le tableau.
-
Appeler quicksort pour trier le tableau. La fonction quicksort utilise
une fonction de comparaison que vous devez écrire, et qui compare
deux éléments du tableau (faire man quicksort).
Dans notre cas les éléments sont des indices, à
partir de là, vous pouvez retrouver le Z dans le repère caméra
de la face , comparer la distance de deux facettes et décider laquelle
est la plus proche. Vous prendrez comme point de référence
celui que vous voulez (un sommet, le barycentre, à vous de voir).
-
Une fois le tableau trié, il suffit de refaire une seconde boucle
et d'afficher en face pleines (fonction FillFace) les faces de la plus
éloignée à la plus proche.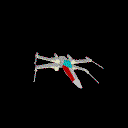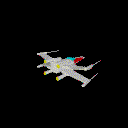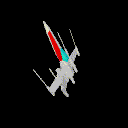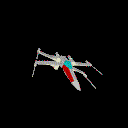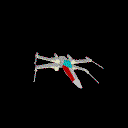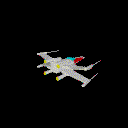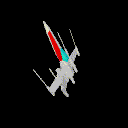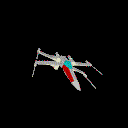
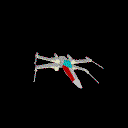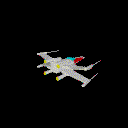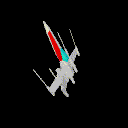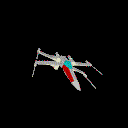
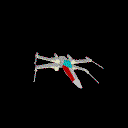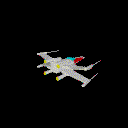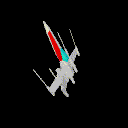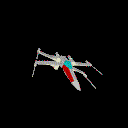
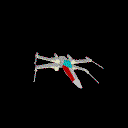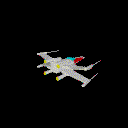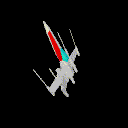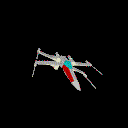Bonne chance !